题目内容
甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,其中a,b∈{1,2,3,4,5,6},若|a-b|≤1,就称甲乙“心相近”.现任意找两人玩这个游戏,则他们“心相近”的概率为 ( )
A. | B. | C. | D. |
D.
解析试题分析:试验包含的所有事件共有6×6=36种猜数的结果。
其中满足题设条件的有如下情形:
若a=1,则b=1,2;他们“心相近”的概率为
若a=2,则b=1,2,3;
若a=3,则b=2,3,4;
若a=4,则b=3,4,5;
若a=5,则b=4,5,6;
若a=6,则b=5,6;
共16种.
故他们“心相近”的概率为 .
.
考点:新定义及概率.

练习册系列答案
相关题目
已知随机变量X~B(6,0.4),则当η=-2X+1时,D(η)=( )
| A.-1.88 | B.-2.88 | C.5. 76 | D.6.76 |
已知事件 与事件
与事件 发生的概率分别为
发生的概率分别为 、
、 ,有下列命题:
,有下列命题:
①若 为必然事件,则
为必然事件,则 ; ②若
; ②若 与
与 互斥,则
互斥,则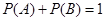 ;
;
③若 与
与 互斥,则
互斥,则 .
.
其中真命题有( )个
| A.0 | B.1 | C.2 | D.3 |
甲乙两名学生通过某种听力测试的概率分别为 ,两人同时参加测试,其中有且只有一人通过的概率为( )
,两人同时参加测试,其中有且只有一人通过的概率为( )
A. | B. | C. | D. |
从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是( )
| A.“至少有一个黑球”与“都是黑球” |
| B.“至少有一个黑球”与“都是红球” |
| C.“至少有一个黑球”与“至少有一个红球” |
| D.“恰有一个黑球”与“恰有两个黑球” |
已知 ,若向区域
,若向区域 内随机投一点
内随机投一点 ,则点
,则点 落在区域
落在区域 内的概率为( )
内的概率为( )
A. | B. | C. | D. |
已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)等于( )
| A.0.6 | B.0.4 | C.0.3 | D.0.2 |
 B.
B. C.
C. D.
D.
 的概率是( ).
的概率是( ).


