题目内容
18、设异面直线a与b所成的角为50°,O为空间一定点,试讨论,过点O与a、b所成的角都是θ(0°≤θ≤90°)的直线l有且仅有几条?
分析:为了讨论:过点O与a、b所成的角都是θ(0°≤θ≤90°)的直线l有且仅有几条,先将涉及到的线放置在同一个平面内观察,如图产,只须考虑过点O与直线a1、b1所成的角都是θ(0°≤θ≤90°)的直线l有且仅有几条即可,再利用cosθ=cosθ1•cosθ2.进行角之间的大小比较即得.
解答: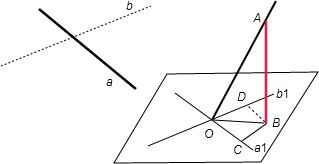 解:过点O作a1∥a,b1∥b,则相交直线a1、b1确定一平面α.a1与b1夹角为50°或130°,设直线OA与a1、b1均为θ角,作AB⊥面α于点B,BC⊥a1于点C,BD⊥b1于点D,记∠AOB=θ1,∠BOC=θ2(θ2=25°或65°),则有cosθ=cosθ1•cosθ2.因为0°≤θ1≤90°,所以0≤cosθ≤cosθ2.
解:过点O作a1∥a,b1∥b,则相交直线a1、b1确定一平面α.a1与b1夹角为50°或130°,设直线OA与a1、b1均为θ角,作AB⊥面α于点B,BC⊥a1于点C,BD⊥b1于点D,记∠AOB=θ1,∠BOC=θ2(θ2=25°或65°),则有cosθ=cosθ1•cosθ2.因为0°≤θ1≤90°,所以0≤cosθ≤cosθ2.
当θ2=25°时,由0≤cosθ≤cos25°,得25°≤θ≤90°;
当θ2=65°时,由0≤cosθ≤cos65°,得65°≤θ≤90°.
故当θ<25°时,直线l不存在;当θ=25°时,直线l有且仅有1条;
当25°<θ<65°时,直线l有且仅有2条;
当θ=65°时,直线l有且仅有3条;
当65°<θ<90°时,直线l有且仅有4条;
当θ=90°时,直线l有且仅有1条.
 解:过点O作a1∥a,b1∥b,则相交直线a1、b1确定一平面α.a1与b1夹角为50°或130°,设直线OA与a1、b1均为θ角,作AB⊥面α于点B,BC⊥a1于点C,BD⊥b1于点D,记∠AOB=θ1,∠BOC=θ2(θ2=25°或65°),则有cosθ=cosθ1•cosθ2.因为0°≤θ1≤90°,所以0≤cosθ≤cosθ2.
解:过点O作a1∥a,b1∥b,则相交直线a1、b1确定一平面α.a1与b1夹角为50°或130°,设直线OA与a1、b1均为θ角,作AB⊥面α于点B,BC⊥a1于点C,BD⊥b1于点D,记∠AOB=θ1,∠BOC=θ2(θ2=25°或65°),则有cosθ=cosθ1•cosθ2.因为0°≤θ1≤90°,所以0≤cosθ≤cosθ2.当θ2=25°时,由0≤cosθ≤cos25°,得25°≤θ≤90°;
当θ2=65°时,由0≤cosθ≤cos65°,得65°≤θ≤90°.
故当θ<25°时,直线l不存在;当θ=25°时,直线l有且仅有1条;
当25°<θ<65°时,直线l有且仅有2条;
当θ=65°时,直线l有且仅有3条;
当65°<θ<90°时,直线l有且仅有4条;
当θ=90°时,直线l有且仅有1条.
点评:本题主要考查了异面直线及其所成的角,以及空间想象力、转化思想方法,属于基础题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目