题目内容
18.已知f(x)对任意x∈[0,+∞),都有f(x+1)=-f(x),当x∈[0,1)时,f(x)=x,若函数g(x)=f(x)-${log}_{{a}^{(x+1)}}$(0<a<1)在区间[0,6]上有3个零点,则实数a的取值范围是( )| A. | [$\frac{1}{7}$,$\frac{1}{5}$) | B. | ($\frac{1}{7}$,$\frac{1}{5}$) | C. | (0,$\frac{1}{7}$) | D. | ($\frac{1}{5}$,1) |
分析 由题意,作出函数y=f(x)在[0,6]的图象,转化函数g(x)=f(x)-${log}_{{a}^{(x+1)}}$(0<a<1)的零点为图象的交点,从而求解.
解答 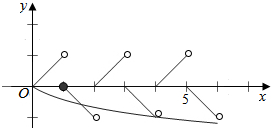 解:∵定义在R上的函数y=f(x),
解:∵定义在R上的函数y=f(x),
对任意x都有f(x+1)=-f(x),
∴f(x+2)=f[(x+1)=1]=-f(x+1)=f(x),
即函数f(x)是周期为2的周期函数,
若函数g(x)=f(x)-${log}_{{a}^{(x+1)}}$(0<a<1)
在区间[0,6]上有3个零点,
则函数y=f(x)与y=loga(x+1)(0<a<1)的图象恰有3个交点,
又由x∈[0,1),f(x)=x,
当x∈[1,2)时,x-1∈[0,1),即有f(x-1)=x-1=-f(x),
即为f(x)=1-x.
在同一坐标系可作出函数y=f(x)
与y=loga(x+1)(0<a<1)在[0,6]的图象如右:
由图可知:函数y=f(x)与y=loga(x+1)(0<a<1)的图象有3个交点时,
当y=loga(x+1)过(4,-1)时,即有loga5=-1,解得a=$\frac{1}{5}$;
当y=loga(x+1)过(6,-1)时,即有loga7=-1,解得a=$\frac{1}{7}$.
由图象可得a的范围是$\frac{1}{7}$≤a<$\frac{1}{5}$.
故选A.
点评 本题考查函数方程的转化思想,考查函数的周期性的运用,同时考查函数的解析式的求法和对数的运算性质,运用数形结合的思想方法是解题的关键.

练习册系列答案
相关题目
10.函数f(x)是定义在(0,+∞)上的单调函数,?x∈(0,+∞),f[f(x)-lnx]=e+1,则方程f(x)-f′(x)=e(其中e为自然对数的底数)的解所在的区间是( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | (2,3) |
 若三角函数f(x)的部分图象如图,则S=f(1)+f(2)+…+f(2017)的值为2017.5.
若三角函数f(x)的部分图象如图,则S=f(1)+f(2)+…+f(2017)的值为2017.5. 的解集为
的解集为 ,则
,则 _______.
_______. 中,已知
中,已知 ,
, ,且
,且 构成等比数列
构成等比数列 的前三项.
的前三项. 的前
的前 项和
项和 .
.