题目内容
已知两点M(4,0),N(-4,0),若曲线上恒存在点P,使|PM|+|PN|=10,则称该曲线为“A型曲线”,给出下列曲线:①y=k(x-4);②y=loga(x-a)(a>0,a≠1);③y=kx3(k∈R);④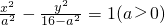 .其中为A型曲线的序号是________.
.其中为A型曲线的序号是________.
①③
分析:利用椭圆的定义判断出P在一个椭圆上;利用题中的新定义知,若是“A型曲线”即与椭圆相交即可,对四个曲线分别判断,对于①③由于它们都过椭圆内部的一点,故是;对于②④举反例说明不是.
解答:∵两点M(4,0),N(-4,0),若曲线上恒存在点P,使|PM|+|PN|=10
∴P的轨迹是椭圆
椭圆的方程为
有“A型曲线”的定义知,若是“A型曲线”即与椭圆相交即可
对于①,直线过(4,0)点,而(4,0)在椭圆的内部,所以直线与椭圆必相交,故①是
对于②,例如当a=100时,对数函数的图象与椭圆不能相交,故②不是
对于③,曲线过(0,0)而(0,0)在椭圆内部,所以相交,故③是
对于④,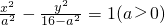 ,例如a2=100时,方程表示的是已知椭圆外部的椭圆,两个椭圆没有交点,所以④不是.
,例如a2=100时,方程表示的是已知椭圆外部的椭圆,两个椭圆没有交点,所以④不是.
故答案为:①③
点评:本题考查椭圆的定义、考查理解题中的新定义.新定义题是近几年常考的题型,要重视.
分析:利用椭圆的定义判断出P在一个椭圆上;利用题中的新定义知,若是“A型曲线”即与椭圆相交即可,对四个曲线分别判断,对于①③由于它们都过椭圆内部的一点,故是;对于②④举反例说明不是.
解答:∵两点M(4,0),N(-4,0),若曲线上恒存在点P,使|PM|+|PN|=10
∴P的轨迹是椭圆
椭圆的方程为

有“A型曲线”的定义知,若是“A型曲线”即与椭圆相交即可
对于①,直线过(4,0)点,而(4,0)在椭圆的内部,所以直线与椭圆必相交,故①是
对于②,例如当a=100时,对数函数的图象与椭圆不能相交,故②不是
对于③,曲线过(0,0)而(0,0)在椭圆内部,所以相交,故③是
对于④,
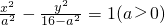 ,例如a2=100时,方程表示的是已知椭圆外部的椭圆,两个椭圆没有交点,所以④不是.
,例如a2=100时,方程表示的是已知椭圆外部的椭圆,两个椭圆没有交点,所以④不是.故答案为:①③
点评:本题考查椭圆的定义、考查理解题中的新定义.新定义题是近几年常考的题型,要重视.

练习册系列答案
相关题目