题目内容
【题目】如图,已知四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,点M在AB上,且AM:MB=1:2,E为PB的中点. 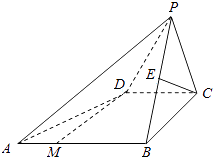
(1)求证:CE∥平面ADP;
(2)求证:平面PAD⊥平面PAB;
(3)棱AP上是否存在一点N,使得平面DMN⊥平面ABCD,若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(1)证明:取棱AP中点F,连接DF,EF.
∵EF为△PAB的中位线,∴EF∥AB,且 ![]()
∵CD∥AB,且 ![]() ,∴EF∥CD,且EF=CD,
,∴EF∥CD,且EF=CD,
∴四边形EFDC为平行四边形,∴CE∥DF
∵DF平面ADP,CE平面ADP,
∴CE∥平面ADP
(2)证明:由(1)可得CE∥DF
∵PC=BC,E为PB的中点,∴CE⊥PB
∵AB⊥BC,平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,AB平面ABCD
∴AB⊥平面PBC
又∵CE平面PBC,
∴AB⊥CE
又∵CE⊥PB,AB∩PB=B,AB,PB平面PBC,
∴CE⊥平面PAB
∵CN∥DF,
∴DF⊥平面PAB
又∵DF平面PAD,
∴平面PAD⊥平面PAB
(3)解:存在, ![]() .
.
证明:取BC中点O,连结AO交MD于Q,连结NQ,
在平面ABCD中由平几得 ![]() ,∴
,∴ ![]() ∥OP.
∥OP.
∵O为等腰△PBC底边上的中点,∴PO⊥BC,
∵PBC⊥底面ABCD,PO平面PBC,平面PBC∩平面ABCD=BC,
∴PO⊥平面ABCD,∴NQ⊥平面ABCD,
∵NQ平面DMN,∴平面DMN⊥平面ABC.
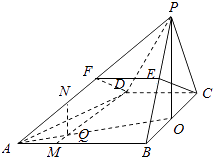
【解析】(1)取棱AP中点F,连接DF,EF,证明四边形EFDC为平行四边形,可得CE∥DF,即可证明CE∥平面ADP;(2)证明CE⊥平面PAB,利用CN∥DF,可得DF⊥平面PAB,即可证明平面PAD⊥平面PAB;(3)存在, ![]() .取BC中点O,连结AO交MD于Q,连结NQ,证明NQ⊥平面ABCD,即可得出结论.
.取BC中点O,连结AO交MD于Q,连结NQ,证明NQ⊥平面ABCD,即可得出结论.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案