Question

（2013•大兴区一模）已知动点P到点A（-2，0）与点B（2，0）的斜率之积为-

1

4

，点P的轨迹为曲线C．
（Ⅰ）求曲线C的方程；
（Ⅱ）若点Q为曲线C上的一点，直线AQ，BQ与直线x=4分别交于M、N两点，直线BM与椭圆的交点为D．求线段MN长度的最小值．

Answer 1

分析：（I）设P（x，y），由题意知利用斜率计算公式即可得到

y

x+2

•

y

x-2

=-

1

4

(x≠±2)，化简即可；
（2）思路一：满足题意的直线AQ的斜率显然存在且不为零，设其方程为y=k（x+2），由（Ⅰ）知kQB•k=

-1

4

，所以，设直线QB方程为y=

-1

4k

（x-2），分别求出点M，N的坐标，再利用两点间的距离公式即可得到|MN|，利用基本不等式的性质即可得出；
思路二：满足题意的直线AQ的斜率显然存在且不为零，设其方程为y=k（x+2），与椭圆的方程联立，可得到根与系数的关系．设Q（x₀，y₀），M（x₁，y₁），N（x₂，y₂），即可得到直线BQ的斜率，以下同思路一；
思路三：设Q（x₀，y₀），则直线AQ的方程为y=

y0

x0+2

(x+2)，直线BQ的方程为y=

y0

x0-2

(x-2)，即可得到点M，N的坐标，利用两点间的距离公式即可得到|MN|，利用导数即可得出．

解答：解：（Ⅰ）设P（x，y），由题意知  kAP•kBP=-

1

4

，即

y

x+2

•

y

x-2

=-

1

4

(x≠±2)
化简得曲线C方程为：

x2

4

+y2=1(x≠±2)
（Ⅱ）思路一
满足题意的直线AQ的斜率显然存在且不为零，设其方程为y=k（x+2），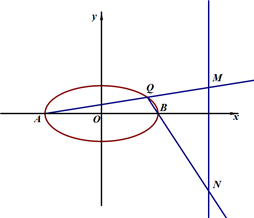
由（Ⅰ）知kQB•k=

-1

4

，所以，设直线QB方程为y=

-1

4k

（x-2），
当x=4时得N点坐标为N(4，

-1

2k

)，易求M点坐标为M（4，6k）
所以|MN|=|6k+

1

2k

|=|6k|+

1

|2k|

≥2

|6k|• 1 |2k|

=2

3

，
当且仅当k=±

3

6

时，线段MN的长度有最小值2

3

．
思路二：满足题意的直线AQ的斜率显然存在且不为零，设其方程为y=k（x+2），
联立方程：

x2 4 +y2=1 y=k(x+2)

消元得（4k²+1）x²+16k²x+16k²-4=0，
设Q（x₀，y₀），M（x₁，y₁），N（x₂，y₂），
由韦达定理得：-2•x0=

16k2-4

4k2+1

，
所以x0=

-8k2+2

4k2+1

，代入直线方程得y0=

4k

4k2+1

，
所以Q(

2-8k2

1+4k2

，

4k

1+4k2

)，又B（2，0）
所以直线BQ的斜率为，

4k 1+4k2 -0

2-8k2 1+4k2 -2

=-

1

4k

以下同思路一
思路三：设Q（x₀，y₀），则直线AQ的方程为y=

y0

x0+2

(x+2)
直线BQ的方程为y=

y0

x0-2

(x-2)
当x=4，得yM=

6y0

x0+2

，即M(4，

6y0

x0+2

)
当x=4，得yN=

2y0

x0-2

，即N(4，

2y0

x0-2

)
则|MN|=|

6y0

x0+2

-

2y0

x0-2

|=|2y0•

2x0-8

x02-4

||MN|2=4y02•(

2x0-8

x02-4

)2
又x02+4y02=4
所以|MN|2=

4(x0-4)2

4-x02

利用导数，或变形为二次函数求其最小值．

点评：本题综合考查了椭圆的标准方程、直线与椭圆相交问题转化为方程联立得到根与系数的关系、斜率计算公式、两点间的距离公式、基本不等式或利用导数研究函数的单调性极值、多角度解决问题等基础知识与基本技能，需要较强的推理能力和计算能力．