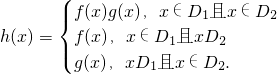题目内容
对定义域分别为D1，D2的函数y=f（x），y=g（x），规定：函数
若f（x）=-2x+3（x≥1），g（x）=x-2（x≤2），则h（x）的解析式h（x）= ．
【答案】分析：由题中所给的新定义函数，根据其规则结合f（x）=-2x+3（x≥1），g（x）=x-2（x≤2），直接写出h（x）的解析式即可得到答案
解答：解：由题意，函数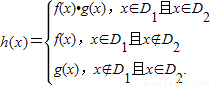
∵f（x）=-2x+3（x≥1），g（x）=x-2（x≤2），
∴h（x）的解析式h（x）=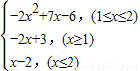
故答案为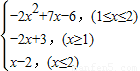
点评：本题是一个新定义的题，此类题解答的关键是理解新定义，根据新定义的规则进行变形可计算得到答案
解答：解：由题意，函数
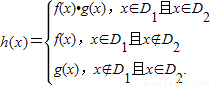
∵f（x）=-2x+3（x≥1），g（x）=x-2（x≤2），
∴h（x）的解析式h（x）=
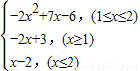
故答案为
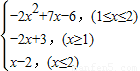
点评：本题是一个新定义的题，此类题解答的关键是理解新定义，根据新定义的规则进行变形可计算得到答案
练习册系列答案
相关题目
