题目内容
过抛物线y=2px(p>0)焦点的一条直线和此抛物线相交,两个人交点的分别为A(x1,y1),B(x2,y2),试求x1•x2的值和y1•y2的值.
【答案】分析: ,由
,由 得到交点坐标,从而得到x1•x2的值和y1•y2的值.
得到交点坐标,从而得到x1•x2的值和y1•y2的值.
 ,由
,由 得
得 .由此能够得到y1•y2的值和x1•x2的值.
.由此能够得到y1•y2的值和x1•x2的值.
解答:解: ,
,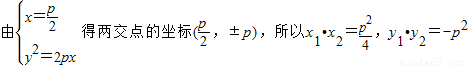 .
.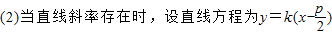 ,
,
由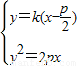 得
得 ,
,
∴y1•y2=-p2,x1•x2= .
.
综上可知, .
.
点评:本题考查直线和抛物线的位置关系的综合运用,解题时要认真审题,注意抛物线性质的灵活运用.
 ,由
,由 得到交点坐标,从而得到x1•x2的值和y1•y2的值.
得到交点坐标,从而得到x1•x2的值和y1•y2的值. ,由
,由 得
得 .由此能够得到y1•y2的值和x1•x2的值.
.由此能够得到y1•y2的值和x1•x2的值.解答:解:
 ,
,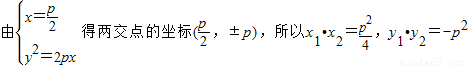 .
.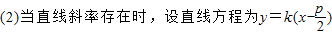 ,
,由
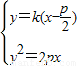 得
得 ,
,∴y1•y2=-p2,x1•x2=
 .
.综上可知,
 .
.点评:本题考查直线和抛物线的位置关系的综合运用,解题时要认真审题,注意抛物线性质的灵活运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目