题目内容
某木材加工厂为了提高生产高效率和产品质量,决定添置一台125000元的新木材加工机器.若机器第x天的维护费为x元,则该机器使用多少天能使平均每天的支出最少?
分析:确定每天的维护费数量,可得总维护费,进而可得总支出费、平均每天的支出,利用基本不等式,即可求得结论.
解答:解:设机器使用x天最经济,则机器每天的维护费数量为1,2,3,…,x(元)
这是一个等差数列,总维护费为
(元),总支出费为125000+
(元)
平均每天的支出为y=
=
+
+
≥2
+
=
当且仅当
=
,即x=500时等号成立.
答:该机器使用500天能使平均每天的支出500.5元为最少.
这是一个等差数列,总维护费为
| x(x+1) |
| 2 |
| x(x+1) |
| 2 |
平均每天的支出为y=
125000+
| ||
| x |
| 125000 |
| x |
| x |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1001 |
| 2 |
当且仅当
| 125000 |
| x |
| x |
| 2 |
答:该机器使用500天能使平均每天的支出500.5元为最少.
点评:本题考查函数模型的构建,考查基本不等式,正确确定函数解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
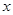 天的维护费为
天的维护费为