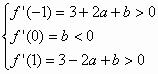Question

若实数m，n为关于x的一元二次方程Ax²＋Bx＋C＝0的两个实数根，则有Ax²＋Bx＋C＝A(x－m)(x－n)，由系数可得：m＋n＝－，且m·n＝．设x₁，x₂，x₃为关于x的方程f(x)＝x³－ax²＋bx－c＝0，(a，b，c∈R)的三个实数根．

(1)写出三次方程的根与系数的关系；即x₁＋x₂＋x₃＝_________；x₁x₂＋x₂x₃＋x₃x₁＝_________；x₁·x₂·x₃＝_________

(2)若a，b，c均大于零，试证明：x₁，x₂，x₃都大于零

(3)若a∈Z，b∈Z，|b|＜2，f(x)在x＝α，x＝β处取得极值，且－1＜α＜β＜1，求方程f(x)＝0三个实根两两不相等时，实数c的取值范围．

Answer 1

答案：
解析：

解：(1)　　 　　(2)由(1)知　即全为正实数或一正两负 　　假设中有一个为正数，两个为负数，不妨设 　　　即　又 　　∴ 　　 　　矛盾， 　　∴都大于零． 　　(3)则的两个不等实根为 　　∵　∴ 　　可得 　　又　∴　∴　又　∴ 　　即 　　令得， 　　即在处取得极大值，在处取得极小值． 　　∵方程三个实根两两不相等， 　　∴　得