题目内容
曲线C:f(x)=x3+ax+b关于坐标原点对称,且与x轴相切.
(1)求a,b的值;
(2)若曲线G:h(x)=λ•
+sinx上存在相互垂直的两条切线,求实数λ的取值范围;
(3)是否存在实数m,n,使函数g(x)=3-|f(x)|的定义域与值域均为[m,n]?并证明你的结论.
(1)求a,b的值;
(2)若曲线G:h(x)=λ•
| f′(x) | x |
(3)是否存在实数m,n,使函数g(x)=3-|f(x)|的定义域与值域均为[m,n]?并证明你的结论.
分析:(1)利用已知条件,说明函数是奇函数,求出b的值,利用函数与x轴相切,求出a的值即可;
(2)利用h(x)=λ•
+sinx的导数,通过曲线上存在相互垂直的两条切线,斜率乘积为-1,通过三角函数的有界性,求实数λ的取值范围;
(3)假设存在m,n符合题意:通过(A)当m<0时,可得
,即m,n是方程g(x)=x的两个相异负根,推出p(x)=x3-x+3(x<3),p′(x)故p(x)至多在(-∞,-
)有一个零点,此时m,n不存在.
通过(B)当m≥0时,因g(x)=3-x3在区间[m,n]上是减函数,利用
⇒
,与条件矛盾,此时m,n不存在
通过(C)当m<0≤n时,说明p(x)=x3-x+3在(-∞,-24]上递增,推出无满足m的解,不存在.
(2)利用h(x)=λ•
| f′(x) |
| x |
(3)假设存在m,n符合题意:通过(A)当m<0时,可得
|
| ||
| 3 |
通过(B)当m≥0时,因g(x)=3-x3在区间[m,n]上是减函数,利用
|
|
通过(C)当m<0≤n时,说明p(x)=x3-x+3在(-∞,-24]上递增,推出无满足m的解,不存在.
解答:解:(1)由f(-x)=-f(x)可得,b=0,
设曲线C与x轴切于T(t,0),
则
⇒
⇒a=t=0⇒f(x)=x3.
(2)h(x)=λ•
+sinx=3λx+sinx,h′(x)=3λ+cosx(x≠0),
设切点(t1,h(t1))(t2,h(t2))⇒h′(t1)•h′(t2)=-1
则(3λ+cost1)(3λ+cost2)=-1,⇒9λ2+3(cost1+cost2)λ+cost1cost2+1=0.
故△=9(cost1+cost2)2-36(cost1cost2+1)≥0⇒(cost1-cost2)2≥4,
又-1≤cost1cost2≤1⇒(cost1-cost2)2≤4⇒cost1-cost2=4,
此时cost1=1,cost2=-1或者cost1=-1,cost2=1可得λ=0.
(3)g(x)=
,假设存在m,n符合题意:
(A)当m<0时,可得
,即m,n是方程g(x)=x的两个相异负根,得x3-x+3=0,
令p(x)=x3-x+3(x<3),p′(x)=3x2-1=0⇒x=-
.
考虑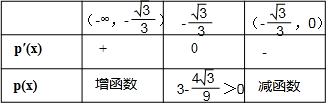
,由于p(0)=3>0,
故p(x)至多在(-∞,-
)有一个零点,此时m,n不存在
(B)当m≥0时,因g(x)=3-x3在区间[m,n]上是减函数,
故
⇒
,
两式相减可得m2+mn+n2=1⇒(m+n)2-mn=1,
由于mn<
⇒(m+n)2-
<1⇒m+n<
由0≤m<n,⇒m<
,n<
⇒m3+n<
<3,与条件矛盾,
此时m,n不存在
(C)当m<0≤n时,因为g(x)max=g(0)=3⇒n=3,
若g(x)min=g(3)=-24⇒m=-24,
,而g(-24)=3-243<g(x)min,矛盾
若g(x)min=g(m)=3+m3⇒3+m3=m (*),
因g(3)=-24≥g(x)min⇒m≤-24,根据情况(A)知p(x)=x3-x+3在(-∞,-24]上递增,
又p(-24)<0,从而方程(*)无满足m≤-24的解,故不存在.
综上所述,不存在实数m,n,使函数的定义域与值域均为[m,n].
设曲线C与x轴切于T(t,0),
则
|
|
(2)h(x)=λ•
| f′(x) |
| x |
设切点(t1,h(t1))(t2,h(t2))⇒h′(t1)•h′(t2)=-1
则(3λ+cost1)(3λ+cost2)=-1,⇒9λ2+3(cost1+cost2)λ+cost1cost2+1=0.
故△=9(cost1+cost2)2-36(cost1cost2+1)≥0⇒(cost1-cost2)2≥4,
又-1≤cost1cost2≤1⇒(cost1-cost2)2≤4⇒cost1-cost2=4,
此时cost1=1,cost2=-1或者cost1=-1,cost2=1可得λ=0.
(3)g(x)=
|
(A)当m<0时,可得
|
令p(x)=x3-x+3(x<3),p′(x)=3x2-1=0⇒x=-
| ||
| 3 |
考虑

,由于p(0)=3>0,
故p(x)至多在(-∞,-
| ||
| 3 |
(B)当m≥0时,因g(x)=3-x3在区间[m,n]上是减函数,
故
|
|
两式相减可得m2+mn+n2=1⇒(m+n)2-mn=1,
由于mn<
| (m+n)2 |
| 4 |
| (m+n)2 |
| 4 |
| 2 | ||
|
由0≤m<n,⇒m<
| 1 | ||
|
| 2 | ||
|
| 7 | ||
3
|
此时m,n不存在
(C)当m<0≤n时,因为g(x)max=g(0)=3⇒n=3,
若g(x)min=g(3)=-24⇒m=-24,
,而g(-24)=3-243<g(x)min,矛盾
若g(x)min=g(m)=3+m3⇒3+m3=m (*),
因g(3)=-24≥g(x)min⇒m≤-24,根据情况(A)知p(x)=x3-x+3在(-∞,-24]上递增,
又p(-24)<0,从而方程(*)无满足m≤-24的解,故不存在.
综上所述,不存在实数m,n,使函数的定义域与值域均为[m,n].
点评:本题考查函数的导数与曲线的切线方程的求法,函数的零点,函数的值域的应用,考查分析问题与解决问题的能力,考查分类讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (a>0),直线l:y=x,在曲线C上有一个动点P,过点P分别作直线l和y轴的垂线,垂足分别为A,B.再过点P作曲线C的切线,分别与直线l和y轴相交于点M,N,O是坐标原点.则△OMN与△ABP的面积之比为 .
(a>0),直线l:y=x,在曲线C上有一个动点P,过点P分别作直线l和y轴的垂线,垂足分别为A,B.再过点P作曲线C的切线,分别与直线l和y轴相交于点M,N,O是坐标原点.则△OMN与△ABP的面积之比为 .