题目内容
某同学参加语文、数学、英语3门课程的考试.假设该同学语文课程取得优秀成绩的概率为 ,数学、英语课程取得优秀成绩的概率分别为m,n(m>n),且该同学3门课程都获得优秀的概率为
,数学、英语课程取得优秀成绩的概率分别为m,n(m>n),且该同学3门课程都获得优秀的概率为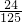 ,该同学3门课程都未获得优秀的概率为
,该同学3门课程都未获得优秀的概率为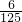 ,且不同课程是否取得优秀成绩相互独立.
,且不同课程是否取得优秀成绩相互独立.
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ) 记ξ为该生取得优秀成绩的课程门数,求ξ的分布列及数学期望Eξ.
解:设事件Ai表示:该生语文、数学、英语课程取得优异成绩,i=1,2,3.
由题意可知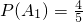 ,P(A2)=m,P(A3)=n
,P(A2)=m,P(A3)=n
(I)由于事件“该生至少有一门课程取得优异成绩”与事件”ξ=0”是对立的,
所以该生至少有一门课程取得优秀成绩的概率是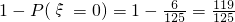
(II)由题意可知,ξ的可能取值为0,1,2,3
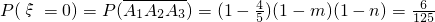 ;
;
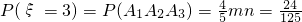 ;
;
解得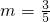 ,
, (m>n).
(m>n).

=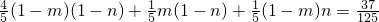
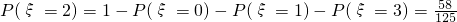 ;
;
∴ξ的分布列为
所以数学期望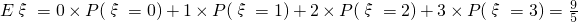 .
.
分析:(I)由于事件“该生至少有一门课程取得优异成绩”与事件”ξ=0”是对立的,计算事件”ξ=0”的概率即可;
(II)由题意可知,ξ的可能取值为0,1,2,3,根据该同学3门课程都获得优秀的概率为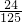 ,该同学3门课程都未获得优秀的概率为
,该同学3门课程都未获得优秀的概率为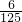 ,确定m,n的值,进而可求ξ的取值为1,2时的概率,即可求得分布列与期望的值.
,确定m,n的值,进而可求ξ的取值为1,2时的概率,即可求得分布列与期望的值.
点评:本题考查对立事件,考查离散型随机事件的分布列与期望,确定变量的取值,计算相应的概率是关键.
由题意可知
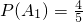 ,P(A2)=m,P(A3)=n
,P(A2)=m,P(A3)=n(I)由于事件“该生至少有一门课程取得优异成绩”与事件”ξ=0”是对立的,
所以该生至少有一门课程取得优秀成绩的概率是
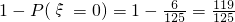
(II)由题意可知,ξ的可能取值为0,1,2,3
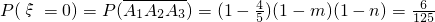 ;
;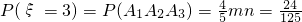 ;
;解得
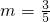 ,
, (m>n).
(m>n).
=
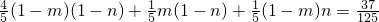
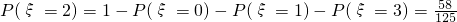 ;
;∴ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | 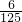 | 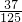 | 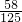 | 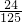 |
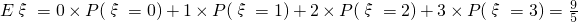 .
.分析:(I)由于事件“该生至少有一门课程取得优异成绩”与事件”ξ=0”是对立的,计算事件”ξ=0”的概率即可;
(II)由题意可知,ξ的可能取值为0,1,2,3,根据该同学3门课程都获得优秀的概率为
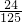 ,该同学3门课程都未获得优秀的概率为
,该同学3门课程都未获得优秀的概率为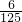 ,确定m,n的值,进而可求ξ的取值为1,2时的概率,即可求得分布列与期望的值.
,确定m,n的值,进而可求ξ的取值为1,2时的概率,即可求得分布列与期望的值.点评:本题考查对立事件,考查离散型随机事件的分布列与期望,确定变量的取值,计算相应的概率是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,数学、英语课程取得优秀成绩的概率分别为m,n(m>n),且该同学3门课程都获得优秀的概率为
,数学、英语课程取得优秀成绩的概率分别为m,n(m>n),且该同学3门课程都获得优秀的概率为 ,该同学3门课程都未获得优秀的概率为
,该同学3门课程都未获得优秀的概率为 ,且不同课程是否取得优秀成绩相互独立.
,且不同课程是否取得优秀成绩相互独立.