题目内容
函数 是定义在
是定义在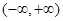 上的奇函数,且
上的奇函数,且 .
.
(1)求实数 的值.(2)用定义证明
的值.(2)用定义证明 在
在 上是增函数;
上是增函数;
(3)写出 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值(无需说明理由)
有无最大值或最小值?如有,写出最大值或最小值(无需说明理由)
 是定义在
是定义在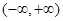 上的奇函数,且
上的奇函数,且 .
.(1)求实数
 的值.(2)用定义证明
的值.(2)用定义证明 在
在 上是增函数;
上是增函数;(3)写出
 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值(无需说明理由)
有无最大值或最小值?如有,写出最大值或最小值(无需说明理由)(1)∵ 是奇函数,∴
是奇函数,∴

∴ ∴
∴ ---------------3分
---------------3分
故 又 ∵
又 ∵ , ∴
, ∴  --------5分
--------5分
∴ -----------------------6分
-----------------------6分
(2)任取 ,
,

∵ ∴
∴ ,
, ,
, ,
,
 ,
, ∴
∴ 即
即
∴ 在
在 上是增函数. ----------10分
上是增函数. ----------10分
(3)单调减区间为 ;
;
当 时,
时, ;当
;当 时,
时, .
.
 是奇函数,∴
是奇函数,∴

∴
 ∴
∴ ---------------3分
---------------3分故
 又 ∵
又 ∵ , ∴
, ∴  --------5分
--------5分∴
 -----------------------6分
-----------------------6分(2)任取
 ,
,
∵
 ∴
∴ ,
, ,
, ,
, ,
, ∴
∴ 即
即
∴
 在
在 上是增函数. ----------10分
上是增函数. ----------10分(3)单调减区间为
 ;
;当
 时,
时, ;当
;当 时,
时, .
.略

练习册系列答案
相关题目
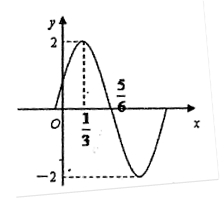
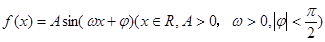 的图象(部分)如图所示,则
的图象(部分)如图所示,则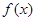 的解析式是
的解析式是



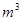 ,深为2
,深为2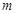 的长方体无盖水池,池底和池壁的造价每平方米分别为240元和160元,那么水池的最低总造价为 元。
的长方体无盖水池,池底和池壁的造价每平方米分别为240元和160元,那么水池的最低总造价为 元。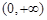 的单调函数
的单调函数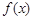 满足:
满足: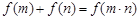 对任意
对任意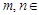
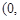
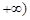 均成立.
均成立. 且
且 ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )



 在区间
在区间 上是减函数,则实数
上是减函数,则实数 的取值范围( )
的取值范围( )



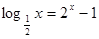 的实数根的个数为( )
的实数根的个数为( )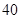 元,若销售价为
元,若销售价为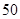 元,可卖出
元,可卖出 元,销售量就减少
元,销售量就减少 ,其中k.b均为常数.当关税税率为75%时,若市场价格为5千元,则市场供应量约为1万件;若市场价格为7千元,则市场供应量约为2万件.
,其中k.b均为常数.当关税税率为75%时,若市场价格为5千元,则市场供应量约为1万件;若市场价格为7千元,则市场供应量约为2万件. .P = q时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率
.P = q时,市场价格称为市场平衡价格.当市场平衡价格不超过4千元时,试确定关税税率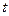 的最大值.
的最大值.