题目内容
已知定义域为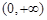 的单调函数
的单调函数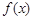 满足:
满足: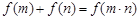 对任意
对任意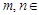
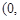
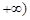 均成立.
均成立.
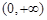 的单调函数
的单调函数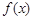 满足:
满足: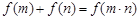 对任意
对任意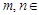
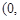
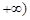 均成立.
均成立.(Ⅰ)令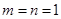 ,解得
,解得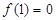 ……………………………………2分
……………………………………2分

又令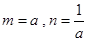 ,解得
,解得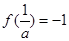 …………………………………………………5分
…………………………………………………5分
(Ⅱ )令
)令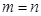 ,得:
,得: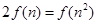 ,所求方程等价于
,所求方程等价于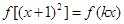 ,又
,又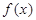 是
是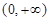 上的单调函数,所以原方程
上的单调函数,所以原方程 可化为
可化为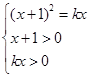 ,即
,即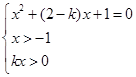 ….…………8分
….…………8分
若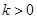 ,则原问题为方程
,则原问题为方程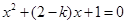 在
在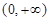 上有一个根,设其两根为
上有一个根,设其两根为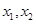 ,则
,则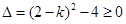 ,
, 又注意到
又注意到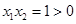 ,
,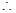 只可能是二重正根,由
只可能是二重正根,由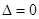 解得
解得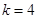 或
或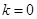 (矛盾,舍去)
(矛盾,舍去)
若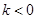 ,则原问题为方程
,则原问题为方程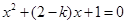 在
在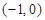 上有一个根,仍有
上有一个根,仍有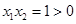 ,记
,记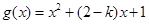 ,易知
,易知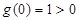 ,由根的分布原理,只需
,由根的分布原理,只需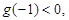 即
即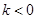 ,综上,
,综上,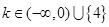 ……………………………………………………….12分
……………………………………………………….12分
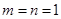 ,解得
,解得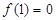 ……………………………………2分
……………………………………2分
又令
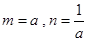 ,解得
,解得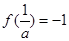 …………………………………………………5分
…………………………………………………5分(Ⅱ
 )令
)令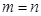 ,得:
,得: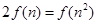 ,所求方程等价于
,所求方程等价于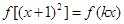 ,又
,又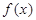 是
是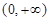 上的单调函数,所以原方程
上的单调函数,所以原方程 可化为
可化为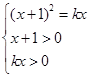 ,即
,即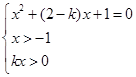 ….…………8分
….…………8分若
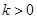 ,则原问题为方程
,则原问题为方程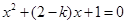 在
在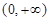 上有一个根,设其两根为
上有一个根,设其两根为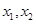 ,则
,则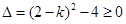 ,
, 又注意到
又注意到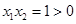 ,
,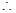 只可能是二重正根,由
只可能是二重正根,由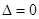 解得
解得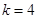 或
或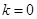 (矛盾,舍去)
(矛盾,舍去)若
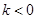 ,则原问题为方程
,则原问题为方程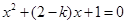 在
在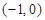 上有一个根,仍有
上有一个根,仍有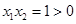 ,记
,记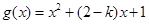 ,易知
,易知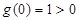 ,由根的分布原理,只需
,由根的分布原理,只需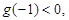 即
即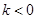 ,综上,
,综上,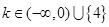 ……………………………………………………….12分
……………………………………………………….12分略

练习册系列答案
相关题目
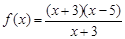 ,
,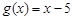 ;
;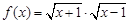 ,
,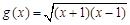 ;
;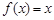 ,
,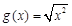 ;
;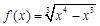 ,
,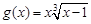
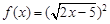 ,
,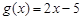
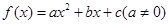 满足条件:①当
满足条件:①当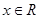 时,
时,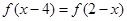 ,且
,且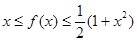 ;②
;② 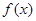 在
在 上的最小值为
上的最小值为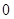 。(1)求
。(1)求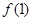 的值及
的值及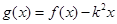 在
在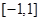 上是单调函数,求
上是单调函数,求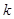 的取值范围;(3)求最大值
的取值范围;(3)求最大值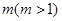 ,使得存在
,使得存在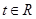 ,只要
,只要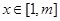 ,就有
,就有 。
。
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
. 的值.(2)用定义证明
的值.(2)用定义证明 在
在 上是增函数;
上是增函数; 上移动时,
上移动时, 的最小值是( )
的最小值是( )

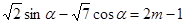 有解,则实数
有解,则实数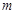 的取值范围是 .
的取值范围是 . 是定义在实数集R上的函数,且
是定义在实数集R上的函数,且
 则
则 ( )
( )


