题目内容
12.已知α为第二象限角.(1)指出$\frac{a}{2}$所在的象限;
(2)若α还满足条件|α+2|≤4,求α的取值区间;
(3)若$\frac{π}{2}$<α<β<π,求α-β的范围.
分析 (1)根据第二象限角的集合的范围即可确定$\frac{a}{2}$所在的象限,
(2)解绝对值不等式可得a∈[-6,2],结合α是第二象限角,可得答案.
(3)先确定-β的范围,再利用不等式的性质,即可得到结论.
解答 解:(1)α为第二象限角,
∴2kπ+$\frac{π}{2}$<α<2kπ+π,k∈Z,
∴kπ+$\frac{π}{4}$<$\frac{α}{2}$<kπ+$\frac{π}{2}$,k∈Z,
当k为偶数时,$\frac{a}{2}$在第一象限,
当k为奇数时,$\frac{a}{2}$在第三象限,
(2)α还满足条件|α+2|≤4,
∴-4≤α+2≤4,
∴-6≤α≤2,
∴a∈($\frac{π}{2}$,2]∪(-$\frac{3π}{2}$,-$\frac{π}{2}$)
(3)∵$\frac{π}{2}$<α<β<π,
∴-π<-β<-$\frac{π}{2}$,
∴-π$+\frac{π}{2}$<α-β<π-$\frac{π}{2}$,
∴-$\frac{π}{2}$<α-β<$\frac{π}{2}$.
点评 本题考查象限角的概念,解题时要熟练掌握象限角的判断方法,属于中档题.

练习册系列答案
相关题目
4.一个几何体的三视图如图所示,则该几何体的体积为( )
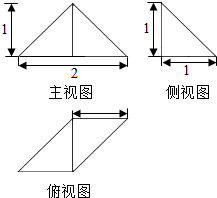

| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
1.设集合A={x|x≥3},B={x|x≤3},则A∩B=( )
| A. | ∅ | B. | R | C. | {x||x≤3} | D. | {3} |