题目内容
叙述并证明直线与平面垂直的判定定理。
解:定理叙述:若一条直线垂直于一个平面内两条相交直线,则该直线与此平面垂直。
证明:已知:直线 ,
, ,求证:a⊥平面π。
,求证:a⊥平面π。
证明:设p是平面π内任意一条直线,则只需证a⊥p,
设直线a,b,c,p的方向向量分别是 ,
,
只需证 ,
,

 ,
,
∴b与c不共线,
直线b,c,p在同一平面π内,
根据平面向量基本定理存在实数λ,μ使得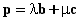 ,
,
则 ,
,
 ,
,
∴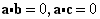 ,
,
∴ ,即
,即 ,
,
所以直线a垂直于平面π。
证明:已知:直线
 ,
, ,求证:a⊥平面π。
,求证:a⊥平面π。 证明:设p是平面π内任意一条直线,则只需证a⊥p,
设直线a,b,c,p的方向向量分别是
 ,
,只需证
 ,
,
 ,
,∴b与c不共线,
直线b,c,p在同一平面π内,
根据平面向量基本定理存在实数λ,μ使得
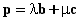 ,
,则
 ,
, ,
,∴
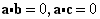 ,
,∴
 ,即
,即 ,
, 所以直线a垂直于平面π。

练习册系列答案
相关题目