题目内容
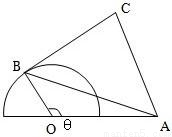
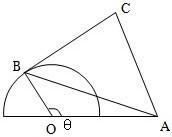
半圆O的直径为2,A为直径延长线上的一点,且OA=2,B为半圆上任意一点,以AB为边向外作等边三角形(如图),问B点在什么位置时,四边形OACB的面积最大,并求出这个最大面积.

【答案】
Smax=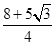 .
.
【解析】
试题分析:设∠AOB=θ,AB=x.
由余弦定理得, x2=12+22-4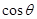 =5-4
=5-4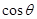 .
.
∴四边形OACB的面积为
S=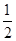 OA
OA OBsin
OBsin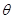 +
+
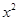 =sin
=sin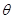 -
- cos
cos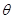 +
+ =2sin(
=2sin(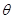 -
- )+
)+ .
.
∵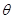 ∈(0,π),∴
∈(0,π),∴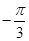 <
<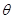
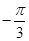 <
<
∴当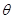
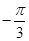 =
=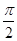 ,即
,即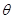 =
=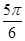 时,Smax=
时,Smax=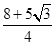 .
.
考点:本题主要考查余弦定理及两角和与差的三角函数公式。
点评:注意数形结合,运用余弦定理构建函数模型,根据角的范围确定函数最值。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
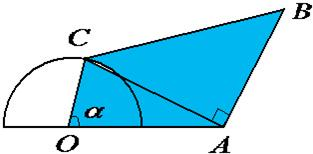 如图,半圆O的直径为2,A为直径延长线上一点,且OA=2,C为半圆上任意一点,以AC为直角边作等腰直角△ABC,求四边形OABC的面积最大值.
如图,半圆O的直径为2,A为直径延长线上一点,且OA=2,C为半圆上任意一点,以AC为直角边作等腰直角△ABC,求四边形OABC的面积最大值.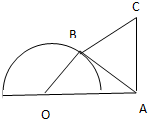 半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB
半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB