Question

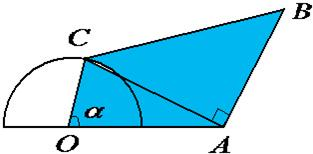如图，半圆O的直径为2，A为直径延长线上一点，且OA=2，C为半圆上任意一点，以AC为直角边作等腰直角△ABC，求四边形OABC的面积最大值．

Answer 1

分析：由余弦定理得AC²=5-4cosα，由四边形OABC的面积为S=S_△AOC+S_△ABC =

5

sin(α-φ)+

5

2

 求得最大值．

解答：解：设∠AOC=α，在△AOC中，
由余弦定理得AC²=5-4cosα，
于是四边形OABC的面积为S=S_△AOC+S_△ABC =

1

2

OA•OCsinα+

1

2

AC2=sinα+

1

2

(5-4cosα)
=sinα-2cosα+

5

2

=

5

sin(α-φ)+

5

2

 
（其中tanφ=2），
故四边形OABC的面积的最大值为

5

+

5

2

．

点评：本题考查余弦定理，两角差的正弦公式的应用，得到四边形OABC的面积为S=S_△AOC+S_△ABC =

5

sin(α-φ)+

5

2

，是解题的关键．