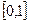题目内容
已知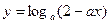 在[0,1]上是
在[0,1]上是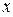 的减函数,则
的减函数,则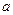 的取值范围是 。
的取值范围是 。
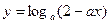 在[0,1]上是
在[0,1]上是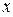 的减函数,则
的减函数,则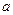 的取值范围是 。
的取值范围是 。1<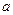 <2
<2
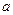 <2
<2∵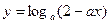 是由
是由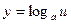 ,
,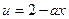 复合而成,又
复合而成,又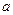 >0
>0
∴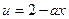 在[0,1]上是
在[0,1]上是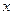 的减函数,由复合函数关系知
的减函数,由复合函数关系知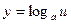 应为增函数,
应为增函数,
∴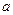 >1
>1
又由于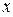 在[0,1]上时
在[0,1]上时 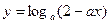 有意义,
有意义,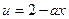 又是减函数,∴
又是减函数,∴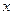 =1时,
=1时,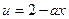 取最小值是
取最小值是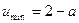 >0即可, ∴
>0即可, ∴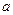 <2
<2
综上可知所求的取值范围是1<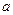 <2
<2
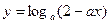 是由
是由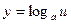 ,
,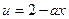 复合而成,又
复合而成,又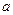 >0
>0∴
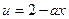 在[0,1]上是
在[0,1]上是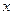 的减函数,由复合函数关系知
的减函数,由复合函数关系知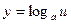 应为增函数,
应为增函数,∴
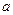 >1
>1又由于
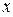 在[0,1]上时
在[0,1]上时 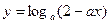 有意义,
有意义,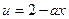 又是减函数,∴
又是减函数,∴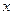 =1时,
=1时,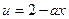 取最小值是
取最小值是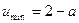 >0即可, ∴
>0即可, ∴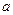 <2
<2综上可知所求的取值范围是1<
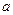 <2
<2
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
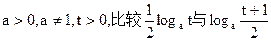 的大小,并证明你的结论
的大小,并证明你的结论
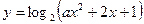 的值域为
的值域为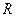 ,则
,则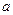 的范围为__________。
的范围为__________。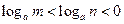 ,则
,则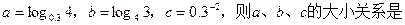
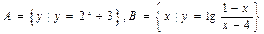 ,则
,则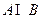 =( )
=( )



 ,当
,当 时的值域为( )
时的值域为( )