题目内容
某种产品的广告费支出 与销售额
与销售额 (单位:万元)之间有下表关系
(单位:万元)之间有下表关系
 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
 与
与 的线性回归方程为
的线性回归方程为 ,当广告支出5万元时,随机误差的效应(残差)为 ( )
,当广告支出5万元时,随机误差的效应(残差)为 ( )A.10 B.20 C.30 D.40
A
解析试题分析:把所给的广告费支出为5百万元时,代入线性回归方程,做出对应的销售额,这是一个预报值,再求出与真实值之间有一个误差即得.解:∵y与x的线性回归方程为 当x=5时,
当x=5时, =50,当广告支出5万元时,由表格得:y=60,故随机误差的效应(残差)为60-50=10,故选A
=50,当广告支出5万元时,由表格得:y=60,故随机误差的效应(残差)为60-50=10,故选A
考点:回归分析
点评:本题考查回归分析的初步应用,考查求线性回归方程,考查预报y的值,是一个综合题目,这种题目完全符合新课标的大纲要求,是一个典型的题目.

练习册系列答案
相关题目
某高校《统计》课程的教师随机给出了选该课程的一些情况,具体数据如下:
| | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
 ,所以可以判定选修统计专业与性别有关.那么这种判断出错的可能性为( )
,所以可以判定选修统计专业与性别有关.那么这种判断出错的可能性为( )A.5% B.95% C.1% D.99%
为了解一片速生林的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出样本的频率分布直方图(如图),那么在这100株树木中,底部周长大于110cm的株数是( )
| A.70 | B.60 |
| C.30 | D.80 |
在建立两个变量 与
与 的回归模型中,分别选择了4个不同模型,他们的相关指数
的回归模型中,分别选择了4个不同模型,他们的相关指数 如下,其中拟合的最好的模型是( )
如下,其中拟合的最好的模型是( )
A.模型1的相关指数 为 为 | B.模型2的相关指数 为 为 |
C.模型3的相关指数 为 为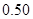 | D.模型4的相关指数 为 为 |
变量x,y有观测数据(xi,yi)(i=1,2,,10),得散点图(1);对变量u,v有观测数据( ui,
vi)(i =1,2,,10),得散点图(2).由这两个散点图可以判断.
| A.变量x与y正相关,u与v正相关 |
| B.变量x与y正相关,u与v负相关 |
| C.变量x与y负相关,u与v正相关 |
| D.变量x与y负相关,u与v负相关 |
 的平均数为h,
的平均数为h, 的平均数为k, 则把两组数据合并成一组以后,这组样本的平均数为( )
的平均数为k, 则把两组数据合并成一组以后,这组样本的平均数为( )



 越大,说明残差平方和越小,模型的拟合效果越好;
越大,说明残差平方和越小,模型的拟合效果越好; 一定过样本点的中心:(
一定过样本点的中心:( ;
; 中的
中的 的值越大,说明“两个分类变量有关系”的可能性越强.
的值越大,说明“两个分类变量有关系”的可能性越强.