题目内容
(本题满分15分)定义在 上的函数
上的函数 ,对任意的
,对任意的 ,
,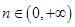 都有
都有 成立,且当
成立,且当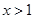 时,
时,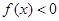 .
.
(1)试求 的值;
的值;
(2)证明: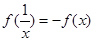 对任意
对任意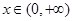 都成立;
都成立;
(3)证明: 在
在 上是减函数;
上是减函数;
(4)当 时,解不等式
时,解不等式 .
.
【答案】
(1)0
(2)证明略
(3)证明略
(4)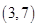
【解析】(1)∵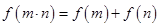 对任意的
对任意的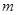 ,
,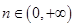 都成立,
都成立,
∴令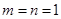 得,
得,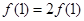 ∴
∴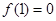 …….3分
…….3分
(2)由题意及(1)可知,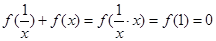
∴ 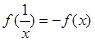 ….6分
….6分
(3)证明:任取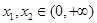 ,且
,且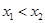 ,[来源:学,科,网]
,[来源:学,科,网]
则 ,
,
且 , 而当
, 而当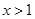 时,
时,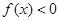 ∴
∴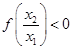 ,[来源:学.科.网]
,[来源:学.科.网]
即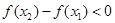 ∴
∴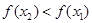 ,
,
即函数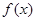 在
在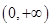 上是减函数;…….10分
上是减函数;…….10分
(4)当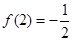 时,
时,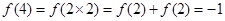
∴原不等式可化为
 由(3)知,
由(3)知,
解得 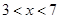 ∴原不等式的解集为
∴原不等式的解集为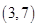 ……15分
……15分

练习册系列答案
相关题目
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆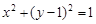 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
|
 且
且 交于点M,求
交于点M,求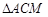 与
与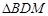 面积之和的最小值.
面积之和的最小值.
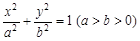 左右焦点
左右焦点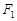 、
、 的动直线l1、l2相交于P点,与椭圆E分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率
的动直线l1、l2相交于P点,与椭圆E分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率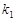 、
、 、
、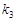 、
、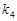 满足
满足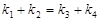 .已知当l1与x轴重合时,
.已知当l1与x轴重合时,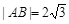 ,
,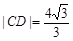 .
.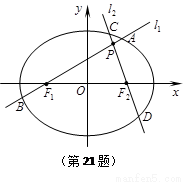
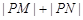 为定值.若存在,求出M、N点坐标,若不存在,说明理由.
为定值.若存在,求出M、N点坐标,若不存在,说明理由.
 (
( )的一个顶点与抛物线 C2:
)的一个顶点与抛物线 C2: 的焦点重合,F1,F2 分别是椭圆的左、右焦点,离心率
的焦点重合,F1,F2 分别是椭圆的左、右焦点,离心率  ,过椭圆右焦点 F2 的直线
,过椭圆右焦点 F2 的直线  与椭圆 C 交于 M,N 两点.
与椭圆 C 交于 M,N 两点. ,若存在,求出直线
,若存在,求出直线
 为定值.
为定值.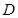 的顶点是椭圆
的顶点是椭圆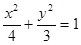 的中心,焦点与该椭圆的右焦点重合.
的中心,焦点与该椭圆的右焦点重合.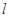 过点
过点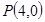 ,交抛物线
,交抛物线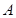 、
、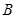 两点.
两点.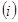 若直线
若直线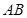 的长;
的长;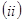 是否存在垂直于
是否存在垂直于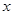 轴的直线
轴的直线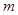 被以
被以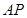 为直径的圆
为直径的圆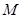 所截得的弦长恒为定值?如果存在,求出
所截得的弦长恒为定值?如果存在,求出 与抛物线
与抛物线 和圆
和圆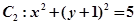 都相切,
都相切, 是
是 的焦点.
的焦点. 与
与 的值;
的值; 是
是 ,直线
,直线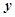 轴于点
轴于点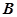 ,以
,以 为邻边作平行四边形
为邻边作平行四边形 ,证明:点
,证明:点 在一条定直线上;
在一条定直线上; ,直线
,直线 ,连接
,连接 交抛物线
交抛物线 两点,求
两点,求 的面积
的面积 的取值范围.
的取值范围.