题目内容
已知一系列的抛物线Cn的方程为y=anx2(n∈N*,an>1),过点An(n,ann2)作该抛物线Cn的切线ln与y轴交于点 Bn,Fn是 Cn的焦点,△AnBnFn的面积为n3
(1)求数列{an}的通项公式;
(2)求证:1+
≤an<2;
(3)设bn=2an-an2,求证:当n≥1时,b1+
b2+
b3+…+
bn<
.
(1)求数列{an}的通项公式;
(2)求证:1+
| ||
| 2 |
(3)设bn=2an-an2,求证:当n≥1时,b1+
| 2 |
| 3 |
| n |
| 3 |
| 4 |
分析:(1)An(n,ann2)在抛物线Cn上,y′=2anx,则切线ln的斜率为2ann,切线方程为 y-ann2=2 ann(x-n).令x=0,得y=-ann2,由此能求出an.
(2)由an=1+
=1+
,{an}为递增数列,由an≥1+
=1+
,由此能证明1+
≤an<2.
(3).由bn=2an-
=
,知b1+
b2+
b3+…+
bn=
(
+
+
+…+
),由此能够证明b1+
b2+
b3+…+
bn<
.
(2)由an=1+
| 1 |
| 2n |
| 4n2-1 |
1-
|
1-
|
| ||
| 2 |
| ||
| 2 |
(3).由bn=2an-
| a | 2 n |
| 1 |
| 4n2 |
| 2 |
| 3 |
| n |
| 1 |
| 4 |
| 1 |
| 12 |
| ||
| 22 |
| ||
| 32 |
| ||
| n2 |
| 2 |
| 3 |
| n |
| 3 |
| 4 |
解答:解:(1)An(n,ann2)在抛物线Cn上,
∵y=anx2,
∴y′=2anx,
则切线ln的斜率为2ann,
切线方程为 y-ann2=2 ann(x-n)…(2分)
令x=0,得y=-ann2,,
∴Bn(0,-ann2),
又Fn(0,
)
∴S_△AnBnFn=
(
+ann2)n=n3
∴
+ann2=2n2,即4n2an2-8n2an+1=0,…(3分)
∴△=64n4-16n2=16n2(4n2-1)>0,
∵an>1,
∴an=1+
…(4分)
(2)证明:∵an=1+
=1+
,
{an}为递增数列,
∴an≥1+
=1+
.…(6分)
又an<1+
=2,
∴1+
≤an<2.…(8分)
(3).证明:bn=2an-
=
…(9分)
∴b1+
b2+
b3+…+
bn=
(
+
+
+…+
)
∵k≥2时,
=
=
<
=
=2(
-
)…(12分)
∴b1+
b2+
b3+…+
bn≤
[1+2(1-
+
-
+…+
-
)]
=
[1+2(1-
)]=
(3-
)<
…(14分)
∵y=anx2,
∴y′=2anx,
则切线ln的斜率为2ann,
切线方程为 y-ann2=2 ann(x-n)…(2分)
令x=0,得y=-ann2,,
∴Bn(0,-ann2),
又Fn(0,
| 1 |
| 4an |
∴S_△AnBnFn=
| 1 |
| 2 |
| 1 |
| 4an |
∴
| 1 |
| 4an |
∴△=64n4-16n2=16n2(4n2-1)>0,
∵an>1,
∴an=1+
| 1 |
| 2n |
| 4n2-1 |
(2)证明:∵an=1+
| 1 |
| 2n |
| 4n2-1 |
1-
|
{an}为递增数列,
∴an≥1+
1-
|
| ||
| 2 |
又an<1+
| 1 |
∴1+
| ||
| 2 |
(3).证明:bn=2an-
| a | 2 n |
| 1 |
| 4n2 |
∴b1+
| 2 |
| 3 |
| n |
| 1 |
| 4 |
| 1 |
| 12 |
| ||
| 22 |
| ||
| 32 |
| ||
| n2 |
∵k≥2时,
| ||
| k2 |
| 1 | ||||||
|
| 2 | ||||||||
(
|
| 2 | ||||||||
(
|
=
2(
| ||||
|
| 1 | ||
|
| 1 | ||
|
∴b1+
| 2 |
| 3 |
| n |
| 1 |
| 4 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
=
| 1 |
| 4 |
| 1 | ||
|
| 1 |
| 4 |
| 2 | ||
|
| 3 |
| 4 |
点评:本题考查数列和解析几何的综合运用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ≤an<2;
≤an<2; .
.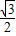 ≤an<2;
≤an<2;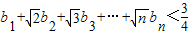 .
.