题目内容
将正方体ABCD—A1B1C1D1的各面涂色，任何相邻两个面不同色，现在有5个不同的颜色，并且涂好了过顶点A的3个面的颜色，那么其余3个面的涂色方案共有（ ）
| A．15种 | B．14种 | C．13种 | D．12种 |
C
本题是一个分类计数问题，设6个面为1对4、2对5、3对6，五种颜色为a、b、c、d、e，且1涂a，2涂b，3涂c，包括5种颜色全都使用和只使用4种颜色时和只使用3种颜色时，做出结果数，根据分类计数原理得到．
解：由题意知本题是一个分类计数问题，
设6个面为1对4、2对5、3对6，五种颜色为a、b、c、d、e，且1涂a，2涂b，3涂c
当5种颜色全都使用时
即只有一组对面颜色相同，设1和4同色，5和6有2种涂法（de或ed）
因为三个面各不相同
所以一共有3×2=6种
当只使用4种颜色时
即有两组对面颜色相同，设1和4同色，2和5同色，6有2种涂法（d或e）共有3×2=6种
当只使用3种颜色时 只能是1和4同色，2和5同色，3和6同色，即只有1种
综上共有6+6+1=13种方法
故选C．
练习册系列答案
相关题目
，女不能排在两端。
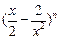的展开式的第三项是常数项，则
="_______. " 
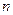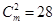，则
等于 （ ）
、
、
、
、
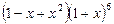展开式中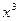
项的系数是_______。