题目内容
已知集合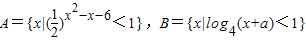
，若A∩B=∅，求实数a的取值范围．
【答案】分析：先利用指、对数不等式的解法分别求出集合A和集合B，再由A∩B=∅，求实数a的取值范围．
解答：解：集合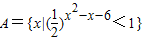
={x|x2-x-6＞0}={x|x＞3或x＜-2}，
B={x|log4（x+a）＜1}={x|0＜x+a＜4}={x|-a＜x＜4-a}，
∵A∩B=∅，
∴
，
解得1≤a≤2．
故实数a的取值范围为：[1，2]．
点评：本题考查指、对数不等式的解法、集合的运算，解题时要认真审题，先分别求出集合A和集合B，再由A∩B=∅，求实数a的取值范围．
解答：解：集合
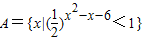={x|x2-x-6＞0}={x|x＞3或x＜-2}，B={x|log4（x+a）＜1}={x|0＜x+a＜4}={x|-a＜x＜4-a}，
∵A∩B=∅，
∴
，解得1≤a≤2．
故实数a的取值范围为：[1，2]．
点评：本题考查指、对数不等式的解法、集合的运算，解题时要认真审题，先分别求出集合A和集合B，再由A∩B=∅，求实数a的取值范围．
练习册系列答案
相关题目
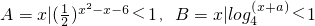，若A∩B=∅，求实数a的取值范围．
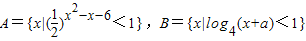，若A∩B=∅，则实数a的取值范围是（ ）
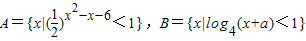，若A∩B=∅，求实数a的取值范围．
，若A∩B=∅，求实数a的取值范围．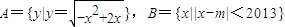
，若A∩B=A，则m的取值范围是（ ）