题目内容
设p：x2-x-2＞0，q：|x-1|＞1，则p是q的（ ）
分析：要想判断两个命题p：x2-x-20＞0，q：|x|-2＞0的关系，我们可以分别求出它们对应解集的集合P和Q，然后判断P和Q的关系．再根据“谁大谁必要，谁小谁充分”的原则，判断命题p与命题q的关系．
解答：解：∵p：x2-x-2＞0，
∴P=（-∞，-1）∪（2，+∞）
又∵q：|x-1|＞1，
∴Q=（-∞，0）∪（2，+∞）
∵Q?P
∴p是q的充分不必要条件
故选B．
∴P=（-∞，-1）∪（2，+∞）
又∵q：|x-1|＞1，
∴Q=（-∞，0）∪（2，+∞）
∵Q?P
∴p是q的充分不必要条件
故选B．
点评：判断一个命题是另一个命题的什么条件，应该先化简各个命题，然后两边互推一下，利用充要条件的有关定义加以判断．
练习册系列答案
名校课堂系列答案
相关题目
设p：x2-x-2＜0，q：
＜0，则p是q的（ ）
| 1+x |
| |x-2| |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
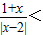0，则p是q的（ ）