题目内容
设p:x2-x-2<0,q:
<0,则p是q的( )
| 1+x |
| |x|-2 |
分析:利用不等式先求出p,q的等价条件,然后利用充分条件和必要条件的定义进行判断.
解答:解:由x2-x-2<0,得-1<x<2,即p:-1<x<2.
由
<0,得(1+x)(|x|-2)<0,
若x≥0,则不等式等价为(1+x)(x-2)<0,解得-1<x<2.此时0≤x<2.
若x<0,则不等式等价为(1+x)(-x-2)<0,
即(1+x)(x+2)>0,解得x>-1或x<-2.此时x<-2或-1<x<0,
综上不等式的解为x<-2或-1<x<2,
即q:x<-2或-1<x<2.
∴p是q的充分不必要条件.
故选:A.
由
| 1+x |
| |x|-2 |
若x≥0,则不等式等价为(1+x)(x-2)<0,解得-1<x<2.此时0≤x<2.
若x<0,则不等式等价为(1+x)(-x-2)<0,
即(1+x)(x+2)>0,解得x>-1或x<-2.此时x<-2或-1<x<0,
综上不等式的解为x<-2或-1<x<2,
即q:x<-2或-1<x<2.
∴p是q的充分不必要条件.
故选:A.
点评:本题主要考查充分条件和必要条件的判断,以及一元二次不等式和分式不等式的解法,比较基础.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
设p:x2-x-2<0,q:
<0,则p是q的( )
| 1+x |
| |x-2| |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
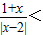 0,则p是q的( )
0,则p是q的( )