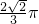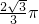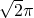题目内容
母线长为1的圆锥体积最大时,其侧面展开图圆心角ϕ等于( )A.
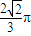
B.
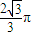
C.

D.
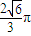
【答案】分析:利用母线长得到底面半径与高的关系,利用圆锥的体积公式将体积表示成底面半径的函数,将函数凑成乘积为定值的形式,利用基本不等式求函数的最值.
解答:解:设圆锥底面半径为r,高为h,则圆锥体积V= πr2•h
πr2•h
又∵r2+h2=1∴h=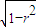
∴圆锥体积V= πr2•
πr2•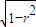 =
=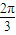 •
•
∵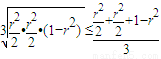 =
= ,
,
当且仅当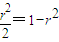 时,即当
时,即当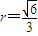 时圆锥体积V取得最大值
时圆锥体积V取得最大值
∴侧面展开图圆心角ϕ=2πr=2π•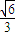
故选择D
点评:本题考查利用基本不等式求函数的最值:需要注意满足的条件:一正;二定;三相等.
解答:解:设圆锥底面半径为r,高为h,则圆锥体积V=
 πr2•h
πr2•h又∵r2+h2=1∴h=
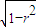
∴圆锥体积V=
 πr2•
πr2•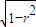 =
=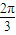 •
•
∵
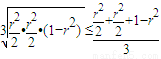 =
= ,
,当且仅当
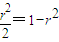 时,即当
时,即当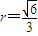 时圆锥体积V取得最大值
时圆锥体积V取得最大值∴侧面展开图圆心角ϕ=2πr=2π•
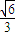
故选择D
点评:本题考查利用基本不等式求函数的最值:需要注意满足的条件:一正;二定;三相等.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
母线长为1的圆锥体积最大时,其侧面展开图圆心角?等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|