题目内容
设函数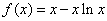 .数列
.数列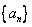 满足
满足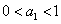 ,
,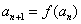 .
.
(Ⅰ)证明:函数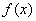 在区间
在区间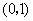 是增函数;
是增函数;
(Ⅱ)证明: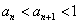 ;
;
(Ⅲ)设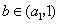 ,整数
,整数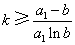 .证明:
.证明: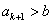 .
.
【答案】
解析:
(Ⅰ)证明: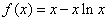 ,
,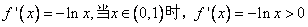
故函数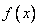 在区间(0,1)上是增函数;
在区间(0,1)上是增函数;
(Ⅱ)证明:(用数学归纳法)(i)当n=1时,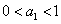 ,
,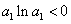 ,
,

由函数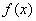 在区间
在区间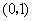 是增函数,且函数
是增函数,且函数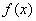 在
在 处连续,则
处连续,则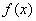 在区间
在区间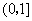 是增函数,
是增函数, ,即
,即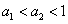 成立;
成立;
(ⅱ)假设当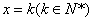 时,
时,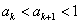 成立,即
成立,即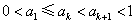
那么当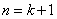 时,由
时,由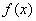 在区间
在区间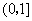 是增函数,
是增函数,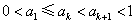 得
得
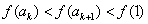 .故
.故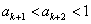 ,即
,即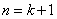 时,
时,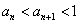 也成立;
也成立;
根据(ⅰ)、(ⅱ)可得对任意的正整数 ,
,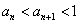 恒成立.
恒成立.
(Ⅲ)证明:若存在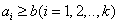 ,则由
,则由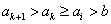 知命题成立。
知命题成立。
若对于任意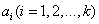 ,均有
,均有 ,则
,则
 …………..(1)
…………..(1)
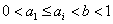 ,故
,故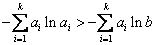 ,又因
,又因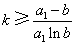 ,即
,即
所以(1)可化为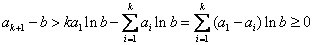 。
。
故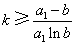 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
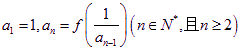 .
.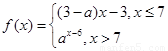 ,数列
,数列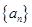 满足
满足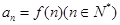 ,且数列
,且数列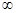 )
D. (2, +
)
D. (2, +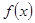 与数列
与数列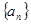 满足关系:(1) a1.>a, 其中a是方程
满足关系:(1) a1.>a, 其中a是方程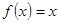 的实根,(2) an+1=
的实根,(2) an+1= ( n
( n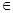 N+
) ,如果
N+
) ,如果 <1
<1  ,数列
,数列 满足
满足 ,且数列
,且数列 的取值范围是_____________________________。
的取值范围是_____________________________。