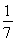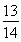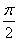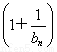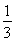题目内容
设数列{an}的前n项和为Sn.已知a1=1,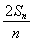 =an+1-
=an+1-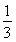 n2-n-
n2-n-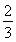 ,n∈N*.
,n∈N*.
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有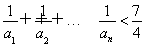 .
.
(1)a2=4.(2)an=n2(n≥2),(3)见解析
【解析】(1)【解析】
∵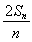 =an+1-
=an+1-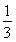 n2-n-
n2-n-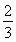 ,n∈N*.
,n∈N*.
∴当n=1时,2a1=2S1=a2-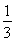 -1-
-1-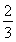 =a2-2.
=a2-2.
又a1=1,∴a2=4.
(2)【解析】
∵ =an+1-
=an+1-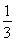 n2-n-
n2-n-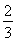 ,n∈N*.
,n∈N*.
∴2Sn=nan+1-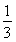 n3-n2-
n3-n2-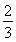 n=nan+1-
n=nan+1-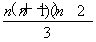 ,①
,①
∴当n≥2时,2Sn-1=(n-1)an-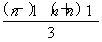 ,②
,②
由①-②,得2Sn-2Sn-1=nan+1-(n-1)an-n(n+1).
∵2an=2Sn-2Sn-1,
∴2an=nan+1-(n-1)an-n(n+1),∴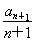 -
-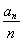 =1.
=1.
∴数列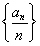 是以首项为
是以首项为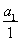 =1,公差为1的等差数列.
=1,公差为1的等差数列.
∴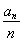 =1+1×(n-1)=n,∴an=n2(n≥2),
=1+1×(n-1)=n,∴an=n2(n≥2),
当n=1时,上式显然成立.∴an=n2,n∈N*.
(3)证明:由(2)知,an=n2,n∈N*,
①当n=1时,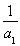 =1<
=1<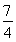 ,∴原不等式成立.
,∴原不等式成立.
②当n=2时,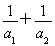 =1+
=1+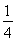 <
<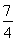 ,∴原不等式亦成立.
,∴原不等式亦成立.
③当n≥3时,∵n2>(n-1)·(n+1),∴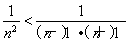 ,
,
∴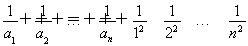
<1+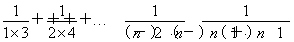
=1+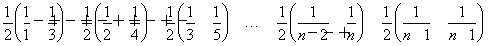
=1+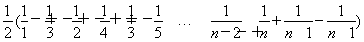
=1+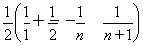 =
=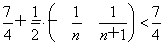 ,
,
∴当n≥3时,原不等式亦成立.
综上,对一切正整数n,有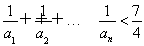 .
.

练习册系列答案
相关题目