题目内容
某人坚持早晨在一条弃用的旧公路上步行锻炼身体,同时数数训练头脑,他先从某地向前走2步后退1步,再向前走4步后退2步,··· ,再向前走 步后退
步后退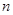 步,··· .当他走完第2008步后就一直往出发地走.此人从出发地到回到原地一共走了 ( )步.
步,··· .当他走完第2008步后就一直往出发地走.此人从出发地到回到原地一共走了 ( )步.
 步后退
步后退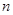 步,··· .当他走完第2008步后就一直往出发地走.此人从出发地到回到原地一共走了 ( )步.
步,··· .当他走完第2008步后就一直往出发地走.此人从出发地到回到原地一共走了 ( )步.| A.3924 | B.3925 | C.3926 | D.3927 |
C
分析:前进的步数是Sn=2(2n-1)后退的步数数Tn=
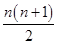 走N次总共走的步数是 2(2n-1)-
走N次总共走的步数是 2(2n-1)- 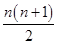 ,故可推出此人走了9次,后退9次后,继续前进,然后返回,从而得解.
,故可推出此人走了9次,后退9次后,继续前进,然后返回,从而得解.解:前进的步数是Sn=2(2n-1)后退的步数数Tn=
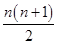 走N次总共走的步数是 2(2n-1)-
走N次总共走的步数是 2(2n-1)-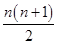 ,
,当n=10时,前进的步子是S10=2046>2008
故此人走了9次,后退9次后,继续前进,然后返回;
去的时候走的步数是2008-
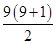 =2008-45=1963,沿原路返回则总步数是2×1963=3926,
=2008-45=1963,沿原路返回则总步数是2×1963=3926,故选C

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 .
.
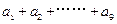 的值为
的值为 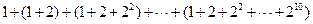 .
.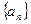 满足
满足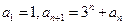 ,则数列
,则数列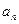 = .
= . 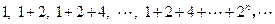 的前n项和为 ( )
的前n项和为 ( )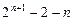
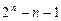
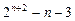
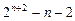
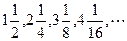 前n项的和为( )
前n项的和为( )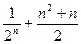
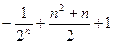
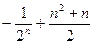
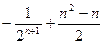
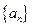 中
中 ,
,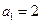 ,
,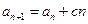 (
(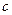 是不为零的常数,
是不为零的常数,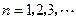 ),且
),且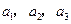 成等比数列.
成等比数列.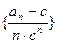 的前
的前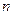 项之和
项之和
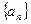 中,
中,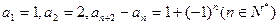 ,则
,则