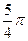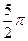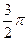题目内容
(本小题12分)已知函数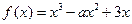 .
.
(I)若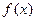 在
在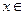 [1,+∞
[1,+∞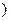 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(II)若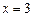 是
是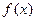 的极值点,求
的极值点,求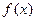 在
在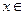 [1,a]上的最小值和最大值.
[1,a]上的最小值和最大值.
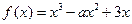 .
.(I)若
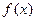 在
在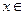 [1,+∞
[1,+∞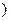 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;(II)若
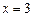 是
是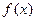 的极值点,求
的极值点,求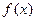 在
在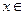 [1,a]上的最小值和最大值.
[1,a]上的最小值和最大值.(I)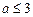
(II)f(x)在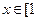 ,
,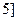 上的最小值是
上的最小值是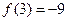 ,最大值是
,最大值是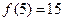 .
.
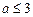
(II)f(x)在
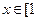 ,
,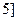 上的最小值是
上的最小值是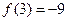 ,最大值是
,最大值是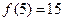 .
.解:(Ⅰ) 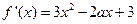 ,要
,要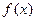 在
在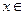 [1,+∞
[1,+∞ 上是增函数,则有
上是增函数,则有
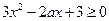 在
在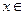 [1,+∞
[1,+∞ 内恒成立,
内恒成立,
即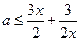 在
在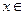 [1,+∞
[1,+∞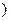 内恒成立
内恒成立
又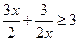 (当且仅当x=1时取等号),所以
(当且仅当x=1时取等号),所以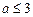
(Ⅱ)由题意知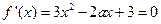 的一个根为
的一个根为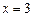 ,可得
,可得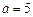 ,
,
所以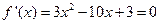 的根为
的根为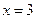 或
或 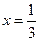 (舍去),
(舍去),
又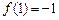 ,
,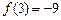 ,
,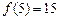 ,
,
∴ f(x)在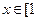 ,
,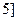 上的最小值是
上的最小值是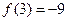 ,最大值是
,最大值是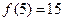 .
.
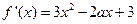 ,要
,要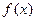 在
在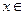 [1,+∞
[1,+∞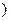 上是增函数,则有
上是增函数,则有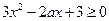 在
在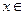 [1,+∞
[1,+∞ 内恒成立,
内恒成立,即
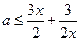 在
在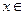 [1,+∞
[1,+∞ 内恒成立
内恒成立又
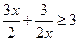 (当且仅当x=1时取等号),所以
(当且仅当x=1时取等号),所以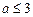
(Ⅱ)由题意知
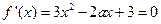 的一个根为
的一个根为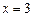 ,可得
,可得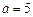 ,
,所以
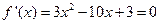 的根为
的根为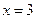 或
或 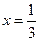 (舍去),
(舍去),又
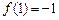 ,
,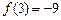 ,
,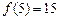 ,
,∴ f(x)在
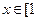 ,
,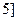 上的最小值是
上的最小值是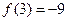 ,最大值是
,最大值是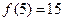 .
.
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
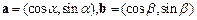 ,其中
,其中 .
.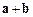 与
与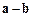 互相垂
互相垂 直;
直;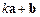 与
与 的长度相等,求
的长度相等,求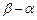 .
.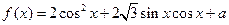 ,
,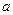 为实常数。
为实常数。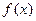 的最小正周期;
的最小正周期; 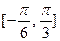 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求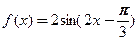 .
. 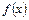 的单调递增区间;
的单调递增区间;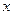 的值.
的值. 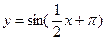 ,
, 的最小正周期为
的最小正周期为 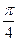
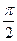
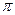
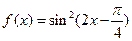 的最小正周期是
的最小正周期是 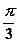
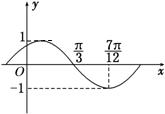
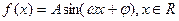 (其中
(其中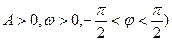 ,其部
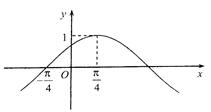
,其部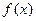 的解析式为 ( )
的解析式为 ( )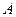 .
.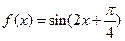
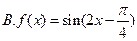
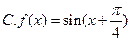
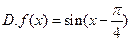
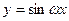 (ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为( )
(ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为( )