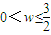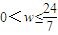题目内容
w是正实数，函数f（x）=2sinwx在[-
，
]上是增函数，那么（ ）
| π |
| 3 |
| π |
| 3 |
分析：由题设函数f（x）=2sinwx在[-
，
]上是增函数可以得出函数的周期T≥
，再由周期公式将此不等式变为
≥
，结合w是正实数即可得出w的取值范围，选出正确选项
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
| 2π |
| w |
| 4π |
| 3 |
解答：解：因为函数f（x）=2sinwx在[-
，
]上是增函数，得到函数的半个周期的长度不小于这个区间的长度，
∴T≥
，即
≥
，
解得w≤
，又w是正实数，
∴0＜w≤
故选A
| π |
| 3 |
| π |
| 3 |
∴T≥
| 4π |
| 3 |
| 2π |
| w |
| 4π |
| 3 |
解得w≤
| 3 |
| 2 |
∴0＜w≤
| 3 |
| 2 |
故选A
点评：本题考查复合三角函数的单调性及三角函数的周期公式，解题的关键是由函数在[-
，
]上是增函数得到周期的取值范围，
| π |
| 3 |
| π |
| 3 |
练习册系列答案
相关题目
上是增函数，那么
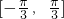上是增函数，那么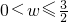
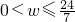
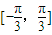上是增函数，那么（ ）
