题目内容
设点P(x,y)(x≥0)为平面直角坐标系xOy中的一个动点(其中O为坐标原点),点P到定点M( ,0)的距离比点P到x轴的距离大
,0)的距离比点P到x轴的距离大 .
.(1)求点P的轨迹方程,并说明它表示什么曲线;
(2)若直线l与点P的轨迹相交于A、B两点,且
 =0,点O到直线l的距离为
=0,点O到直线l的距离为 ,求直线l的方程.
,求直线l的方程.
【答案】分析:(1)用直接法或定义法求得点P轨迹方程为y2=2x,表示以原点为顶点,对称轴为x轴,开口向右的一条抛物线.
(2)当直线l的斜率不存在时,由题设可知直线l的方程是x=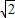 ,联立x=
,联立x=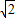 与y2=2x可求得A(
与y2=2x可求得A(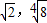 ),B(
),B(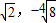 ),不符合
),不符合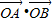 =0.当直线l的斜率存在时,设直线l的方程为y=kx+b(k≠0,b≠0),联立y=kx+b与y2=2x,化简得ky2-2y+2b=0,由此能够求出直线l的方程.
=0.当直线l的斜率存在时,设直线l的方程为y=kx+b(k≠0,b≠0),联立y=kx+b与y2=2x,化简得ky2-2y+2b=0,由此能够求出直线l的方程.
解答:解:(1)由定义法,知点P轨迹方程为y2=2x,
表示以原点为顶点,对称轴为x轴,开口向右的一条抛物线.(6分)
(2)当直线l的斜率不存在时,
由题设可知直线l的方程是x=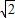 ,
,
联立x=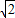 与y2=2x可求得A(
与y2=2x可求得A(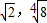 ),B(
),B(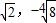 ),
),
不符合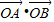 =0 (7分)
=0 (7分)
当直线l的斜率存在时,
设直线l的方程为y=kx+b(k≠0,b≠0),
联立y=kx+b与y2=2x,
化简得ky2-2y+2b=0 (9分)
设A(x1,y1),B(x2,y2),
则y1y2=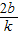
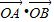 =0?x1x2+y1y2=0?
=0?x1x2+y1y2=0?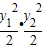 +y1y2=0?y1y2+4=0?
+y1y2=0?y1y2+4=0?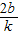 +4=0?b+2k=0 ①(11分)
+4=0?b+2k=0 ①(11分)
又O到直线l距离为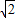 得
得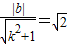 ②(12分)
②(12分)
联立①②解得k=1,b=-2或k=-1,b=2,所以直线l的方程为y=x-2或y=-x+2(13分)
点评:本题考查抛物线的方程的求法和直线方程的求法,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
(2)当直线l的斜率不存在时,由题设可知直线l的方程是x=
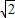 ,联立x=
,联立x=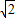 与y2=2x可求得A(
与y2=2x可求得A(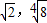 ),B(
),B(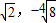 ),不符合
),不符合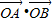 =0.当直线l的斜率存在时,设直线l的方程为y=kx+b(k≠0,b≠0),联立y=kx+b与y2=2x,化简得ky2-2y+2b=0,由此能够求出直线l的方程.
=0.当直线l的斜率存在时,设直线l的方程为y=kx+b(k≠0,b≠0),联立y=kx+b与y2=2x,化简得ky2-2y+2b=0,由此能够求出直线l的方程.解答:解:(1)由定义法,知点P轨迹方程为y2=2x,
表示以原点为顶点,对称轴为x轴,开口向右的一条抛物线.(6分)
(2)当直线l的斜率不存在时,
由题设可知直线l的方程是x=
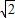 ,
,联立x=
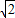 与y2=2x可求得A(
与y2=2x可求得A(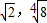 ),B(
),B(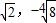 ),
),不符合
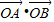 =0 (7分)
=0 (7分)当直线l的斜率存在时,
设直线l的方程为y=kx+b(k≠0,b≠0),
联立y=kx+b与y2=2x,
化简得ky2-2y+2b=0 (9分)
设A(x1,y1),B(x2,y2),
则y1y2=
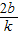
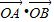 =0?x1x2+y1y2=0?
=0?x1x2+y1y2=0?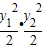 +y1y2=0?y1y2+4=0?
+y1y2=0?y1y2+4=0?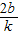 +4=0?b+2k=0 ①(11分)
+4=0?b+2k=0 ①(11分)又O到直线l距离为
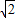 得
得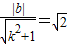 ②(12分)
②(12分)联立①②解得k=1,b=-2或k=-1,b=2,所以直线l的方程为y=x-2或y=-x+2(13分)
点评:本题考查抛物线的方程的求法和直线方程的求法,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,0)的距离比点P到x轴的距离大
,0)的距离比点P到x轴的距离大 .
.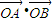 =0,点O到直线l的距离为
=0,点O到直线l的距离为 ,求直线l的方程.
,求直线l的方程.