题目内容
11.若直线y=x+b与曲线x=$\sqrt{1-{y^2}}$恰有一个公共点,则b的取值范围是( )| A. | $[{-\sqrt{2},\sqrt{2}}]$ | B. | $[{-1,\sqrt{2}}]$ | C. | $(-1,1]∪\{\sqrt{2}\}$ | D. | $(-1,1]∪\{-\sqrt{2}\}$ |
分析 曲线x=$\sqrt{1-{y^2}}$即 x2+y2=1(x≥0)表示一个半径为1的半圆,如图,数形结合求得当直线y=x+b与曲线x=$\sqrt{1-{y^2}}$恰有一个公共点时b的取值范围.
解答 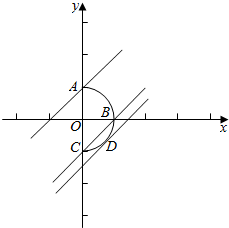 解:曲线x=$\sqrt{1-{y^2}}$即 x2+y2=1(x≥0)表示一个半径为1的半圆,如图所示.
解:曲线x=$\sqrt{1-{y^2}}$即 x2+y2=1(x≥0)表示一个半径为1的半圆,如图所示.
当直线y=x+b经过点A(0,1)时,求得b=1,
当直线y=x+b经过点B(1,0)时,求得b=-1,
当直线和半圆相切于点D时,由圆心O到直线y=x+b的距离等于半径,
可得$\frac{|0-0+b|}{\sqrt{2}}$=1,求得b=-$\sqrt{2}$,或b=$\sqrt{2}$(舍去).
故当直线y=x+b与曲线x=$\sqrt{1-{y^2}}$恰有一个公共点时b的取值范围是-1<b≤1或b=-$\sqrt{2}$,
故选:D.
点评 本题主要考查了直线与圆相交的性质.对于此类问题除了用联立方程转化为方程的根的问题之外,也可用数形结合的方法较为直观,属于基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
1.下列判断正确的是( )
| A. | 函数f(x)=1既是奇函数又是偶函数 | B. | 函数f(x)=(1-x)$\sqrt{\frac{1+x}{1-x}}$是偶函数 | ||
| C. | 函数f(x)=$\frac{{x}^{2}-2x}{x-2}$是奇函数 | D. | 函数f(x)=x+$\sqrt{{x}^{2}-1}$是非奇非偶函数 |
2.若复数(a2-1)+(a-1)i是纯虚数,则实数a的值为( )
| A. | 1 | B. | 0 | C. | 1或-1 | D. | -1 |
19.已知f(x)=$\left\{\begin{array}{l}(2a-1)x+3a,x<1\\{a^x},x≥1\end{array}$满足对任意x1≠x2都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$<0成立,那么a的取值范围是( )
| A. | (0,1) | B. | $(0,\frac{1}{2})$ | C. | $[\frac{1}{4},\frac{1}{2})$ | D. | $[\frac{1}{4},1)$ |