题目内容
函数f(x)的导函数f'(x)=2x+b,且f(0)=c,g(x)=
.
(1)若c>0,g(x)为奇函数,且g(x)的最大值为
求b,c的值;
(2)若函数F(x)=f(x)+2-c定义域为[-1,1],且F(x)的最小值为2,当函数f(x)在区间[-1,1]上有零点,求实数c的取值范围.
| x |
| f(x) |
(1)若c>0,g(x)为奇函数,且g(x)的最大值为
| 1 |
| 2 |
(2)若函数F(x)=f(x)+2-c定义域为[-1,1],且F(x)的最小值为2,当函数f(x)在区间[-1,1]上有零点,求实数c的取值范围.
分析:(1)由条件得出f(x)=x2+bx+c,根据g(x)为奇函数求得b=0,g(x)=
=
,再结合基本不等式求出最大值,列出关于c的方程,即可求得c值.
(2)先配方:F(x)=x2+bx+2=(x+
)2+2-
再对b进行分类讨论:-
>1,当-
<-1,-1≤-
≤1,求得F(x)的最小值得到b值,后根据f(x)=x2+c=0的区间[-1,1]上有解,即可得出c的取值范围.
| x |
| x2+c |
| 1 | ||
x+
|
(2)先配方:F(x)=x2+bx+2=(x+
| b |
| 2 |
| b2 |
| 4 |
| b |
| 2 |
| b |
| 2 |
| b |
| 2 |
解答:解:(1)∵f'(x)=2x+b,且f(0)=c,则f(x)=x2+bx+c,∴g(x)=
=
,
∵g(x)为奇函数,∴g(-x)=-g(x)恒成立,∴b=0,g(x)=
=
∵g(0)=0且x+
∈(-∞,-2
]∪[2
,+∞),∴g(x)∈[-
,
],
由
=
得c=1
(2)F(x)=x2+bx+2=(x+
)2+2-
当-
>1,即b<-2时F(x)min=F(1)=3+b=2得b=-1舍去
当-
<-1,即b>2时F(x)min=F(-1)=3-b=2得b=1舍去-1≤-
≤1即-2≤b≤2F(x)min=F(-
)=2-
=2,得b=0满足条件
∴f(x)=x2+c,由f(x)=x2+c=0得c=-x2,∵x∈[-1,1],∴-x2∈[-1,0]
∵f(x)=x2+c=0的区间[-1,1]上有解,c的取值范围为[-1,0]
| x |
| f(x) |
| x |
| x2+bx+c |
∵g(x)为奇函数,∴g(-x)=-g(x)恒成立,∴b=0,g(x)=
| x |
| x2+c |
| 1 | ||
x+
|
∵g(0)=0且x+
| c |
| x |
| c |
| c |
| 1 | ||
2
|
| 1 | ||
2
|
由
| 1 | ||
2
|
| 1 |
| 2 |
(2)F(x)=x2+bx+2=(x+
| b |
| 2 |
| b2 |
| 4 |
当-
| b |
| 2 |
当-
| b |
| 2 |
| b |
| 2 |
| b |
| 2 |
| b2 |
| 4 |
∴f(x)=x2+c,由f(x)=x2+c=0得c=-x2,∵x∈[-1,1],∴-x2∈[-1,0]
∵f(x)=x2+c=0的区间[-1,1]上有解,c的取值范围为[-1,0]
点评:本小题主要考查导数在最大值、最小值问题中的应用、不等式的解法等基础知识,考查运算求解能力,化归与转化思想.属于基础题.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,
已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,| x | -2 | 0 | 4 |
| f(x) | 1 | -1 | 1 |
| b+3 |
| a+3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-
|
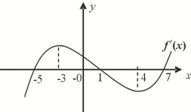 4、已知函数f(x)的导函数的图象如图所示,给出下列四个结论:
4、已知函数f(x)的导函数的图象如图所示,给出下列四个结论: