题目内容
设集合 ,集合
,集合 .若
.若 ,则
,则 .
.

解析试题分析:由 知:
知: ,则
,则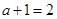 ,解得
,解得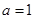 ,则
,则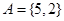 ,
,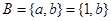 ,由
,由 又知:
又知: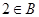 ,则
,则 ,
,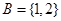 ,所以
,所以 。
。
考点:集合的运算
点评:集合有三种运算:交集、并集和补集。有时在运算前,需对集合进行变化。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
题目内容
设集合 ,集合
,集合 .若
.若 ,则
,则 .
.

解析试题分析:由 知:
知: ,则
,则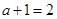 ,解得
,解得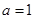 ,则
,则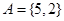 ,
,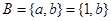 ,由
,由 又知:
又知: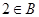 ,则
,则 ,
,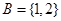 ,所以
,所以 。
。
考点:集合的运算
点评:集合有三种运算:交集、并集和补集。有时在运算前,需对集合进行变化。

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案