题目内容
设集合 ,且满足下列条件:
,且满足下列条件:
(1) ,
, ; (2)
; (2)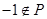 ;
;
(3) 中的元素有正数,也有负数; (4)
中的元素有正数,也有负数; (4) 中存在是奇数的元素.
中存在是奇数的元素.
现给出如下论断:① 可能是有限集;②
可能是有限集;② ,
, ;
;
③ ; ④
; ④ .
.
其中正确的论断是 . (写出所有正确论断的序号)
②③④
解析试题分析:对于论断①,取一个元素 ,满足
,满足 ,且
,且 ,则
,则 ,即
,即 ,
, ,即
,即 ,
, ,依此类推,
,依此类推, ,
, ,故即
,故即 ,
,
且集合 为无限集,故集合
为无限集,故集合 为无限集,论断①不正确;对于论断②,如论断①,在集合
为无限集,论断①不正确;对于论断②,如论断①,在集合 必然能找到一个正整数
必然能找到一个正整数 ,使得
,使得 ,则
,则 ,即论断②正确;对于论断③,
,即论断②正确;对于论断③, ,
, ,
, ,即
,即 ,使得
,使得 ,若
,若 ,则有
,则有 ,则
,则 ,论断③正确;对于论断④,若
,论断③正确;对于论断④,若 ,取
,取 ,则
,则 ,由于
,由于 ,令
,令 ,
, ,
,
由于 中存在是奇数的元素,若
中存在是奇数的元素,若 中存在为正的奇数
中存在为正的奇数 ,则存在
,则存在 ,使得
,使得 ,根据条件(1),则有
,根据条件(1),则有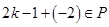 ,即
,即 ,
, ,即
,即 ,
, ,依次类推,
,依次类推, ,即
,即 ,这与条件(2)矛盾,同理,若
,这与条件(2)矛盾,同理,若 中存在为负的奇数,也可以得到
中存在为负的奇数,也可以得到 ,仍与条件(2)矛盾,故论断④正确.
,仍与条件(2)矛盾,故论断④正确.
考点:集合、分析法

练习册系列答案
相关题目
 ,
, ,则集合
,则集合 的所有元素之和为 .
的所有元素之和为 . 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 ,若
,若 ,
, ,则实数
,则实数 的取值范围是
的取值范围是  ,
,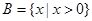 ,则
,则 .
.  ,如果
,如果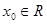 满足:对任意
满足:对任意 ,都存在
,都存在 ,使得
,使得 ,那么称
,那么称 为集合
为集合 的一个聚点,则在下列集合中:(1)
的一个聚点,则在下列集合中:(1) ;(2)
;(2) ;(3)
;(3) ;(4)
;(4) ,以
,以 为聚点的集合有
为聚点的集合有  ,集合
,集合 .若
.若 ,则
,则 .
. =
=