题目内容
对于空间任意一点O和不共线的三点A、B、C,有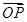 =x
=x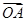 +y
+y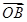 +z
+z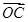 (x、y、z∈R),
(x、y、z∈R),
则x+y+z=1是P、A、B、C四点共面的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
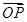 =x
=x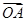 +y
+y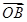 +z
+z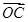 (x、y、z∈R),
(x、y、z∈R),则x+y+z=1是P、A、B、C四点共面的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
C
试题分析:证充分条件:因为x+y+z=1,所以
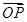 =x
=x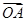 +y
+y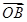 +z
+z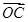 = x
= x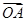 +y
+y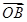 +
+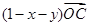 ,所以
,所以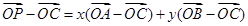 ,即
,即 ,根据平面向量基本定理可知,
,根据平面向量基本定理可知,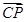 ,
,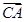 ,
,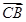 三向量共面,因为有公共点C所以P、A、B、C四点共面。证必要条件:因为P、A、B、C四点共面,所以由平面向量定理可知有且只有一对实数对
三向量共面,因为有公共点C所以P、A、B、C四点共面。证必要条件:因为P、A、B、C四点共面,所以由平面向量定理可知有且只有一对实数对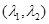 使
使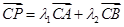 ,由向量减法法则可将上式变形为
,由向量减法法则可将上式变形为 ,整理的
,整理的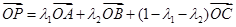 ,所以
,所以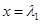 ,
,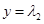 ,
,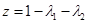 ,
,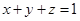 。故C正确。
。故C正确。
练习册系列答案
相关题目
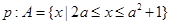 ,条件
,条件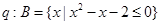 ,若
,若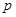 是
是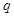 的充分条件,求实数
的充分条件,求实数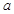 的取值范围.
的取值范围.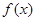 的导函数为
的导函数为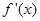 ,那么“
,那么“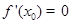 ”是“
”是“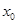 是函数
是函数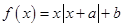 是奇函数的充要条件是( )
是奇函数的充要条件是( )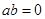
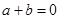
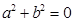
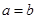
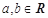 , 则 “
, 则 “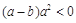 ”是“
”是“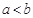 ”的__________.
”的__________.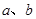 为实数,命题甲:
为实数,命题甲: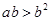 ,命题乙:
,命题乙: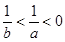 ,则甲是乙的( )条件
,则甲是乙的( )条件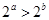 ”是“
”是“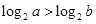 ”的( )
”的( )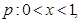
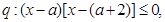 若p是q的充分而不必要条件,则实数a的取值范围是 ( )
若p是q的充分而不必要条件,则实数a的取值范围是 ( )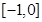

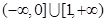
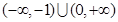
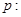
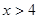 ;命题
;命题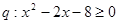 ,那么
,那么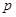 是
是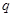 的 条件(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”).
的 条件(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”).