题目内容
(本小题满分10分)如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为 ,转盘(B)指针所对的区域为
,转盘(B)指针所对的区域为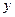 ,
, 、
、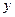

 ,设
,设 +
+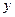 的值为
的值为 ,每一次游戏得到奖励分为
,每一次游戏得到奖励分为 .
.
(Ⅰ)求 <2且
<2且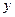 >1的概率;
>1的概率;
(Ⅱ)某人进行了12次游戏,求他平均可以得到的奖励分.
 ,转盘(B)指针所对的区域为
,转盘(B)指针所对的区域为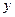 ,
, 、
、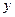

 ,设
,设 +
+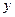 的值为
的值为 ,每一次游戏得到奖励分为
,每一次游戏得到奖励分为 .
. (Ⅰ)求
 <2且
<2且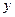 >1的概率;
>1的概率;(Ⅱ)某人进行了12次游戏,求他平均可以得到的奖励分.
(Ⅰ) (Ⅱ) 50
(Ⅱ) 50
 (Ⅱ) 50
(Ⅱ) 50⑴由几何概率模型可知: ;
;
 (2分)
(2分)
则 ,
,
所以 (4分)
(4分)
⑵由条件可知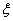 的取值为:
的取值为: ,则
,则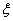 的分布列为:
的分布列为:
(8分)
他平均一次得到的奖励分即为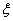 的期望值:
的期望值:

所以给他玩 次,平均可以得到
次,平均可以得到 分 (10分)
分 (10分)
 ;
;  (2分)
(2分)则
 ,
,所以
 (4分)
(4分)⑵由条件可知
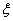 的取值为:
的取值为: ,则
,则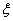 的分布列为:
的分布列为: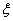 | 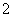 |  |  |  |  |
 |  |  |  | 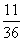 |  |
他平均一次得到的奖励分即为
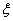 的期望值:
的期望值:
所以给他玩
 次,平均可以得到
次,平均可以得到 分 (10分)
分 (10分)
练习册系列答案
相关题目
 校高三年级学生家庭月平均收入不多于10000元的共有100
校高三年级学生家庭月平均收入不多于10000元的共有100 0人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示.
0人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示.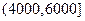 (元)间的每位同学得助学金1500元,家庭收入在
(元)间的每位同学得助学金1500元,家庭收入在 (元)间的每位同学得助学金1000元,家庭收入在
(元)间的每位同学得助学金1000元,家庭收入在 (元)间的同学不发助学金.
(元)间的同学不发助学金.
 元,写出
元,写出 元,求
元,求 .
. 的分布列;
的分布列; 的分布列.
的分布列.
 ,求
,求 .
.