题目内容
设函数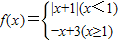 ,则使得f(x)≥1的自变量x的取值范围是( )
,则使得f(x)≥1的自变量x的取值范围是( )A.(-∞,-2]∪[1,2]
B.(-∞,-2)∪(0,2)
C.(-∞,-2]∪[0,2]
D.[-2,0]∪[2,+∞)
【答案】分析:首先分析题目求函数 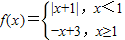 使得f(x)≥1的自变量x的取值范围,因为函数是分段函数,故需要在两段分别做分析讨论,然后求它们的并集即可得到答案.
使得f(x)≥1的自变量x的取值范围,因为函数是分段函数,故需要在两段分别做分析讨论,然后求它们的并集即可得到答案.
解答:解:对于求分段函数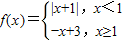 ,f(x)≥1自变量的取值范围.
,f(x)≥1自变量的取值范围.
可以分段求解:
当x<1时候,f(x)=|x+1|≥1,解得x≥0或x≤-2.根据前提条件故0≤x≤1,x≤-2满足条件.
当x≥1时候,f(x)=-x+3≥1,解得x≤2,根据前提条件故1≤x≤2满足条件.
综上所述x的取值范围是x≤-2或0≤x≤2.
故选C.
点评:此题考查了其他不等式的解法,考查了转化的思想以及分类讨论的数学思想.要求学生理解分段函数的意义,即为自变量取值不同,函数解析式不同.
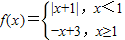 使得f(x)≥1的自变量x的取值范围,因为函数是分段函数,故需要在两段分别做分析讨论,然后求它们的并集即可得到答案.
使得f(x)≥1的自变量x的取值范围,因为函数是分段函数,故需要在两段分别做分析讨论,然后求它们的并集即可得到答案.解答:解:对于求分段函数
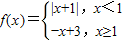 ,f(x)≥1自变量的取值范围.
,f(x)≥1自变量的取值范围.可以分段求解:
当x<1时候,f(x)=|x+1|≥1,解得x≥0或x≤-2.根据前提条件故0≤x≤1,x≤-2满足条件.
当x≥1时候,f(x)=-x+3≥1,解得x≤2,根据前提条件故1≤x≤2满足条件.
综上所述x的取值范围是x≤-2或0≤x≤2.
故选C.
点评:此题考查了其他不等式的解法,考查了转化的思想以及分类讨论的数学思想.要求学生理解分段函数的意义,即为自变量取值不同,函数解析式不同.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
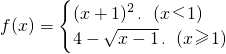 ,则使得f(x)≥1的自变量x的取值范围是________.
,则使得f(x)≥1的自变量x的取值范围是________.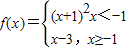 ,则使得f(x)≥1的自变量x的取值范围为 .
,则使得f(x)≥1的自变量x的取值范围为 .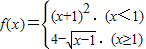 ,则使得f(x)≥1的自变量x的取值范围是 .
,则使得f(x)≥1的自变量x的取值范围是 .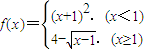 ,则使得f(x)≥1的自变量x的取值范围是 .
,则使得f(x)≥1的自变量x的取值范围是 .