题目内容

（2009•湖北模拟）无论k取何值时，方程|x2-5x+4|=k(x-
5
2
)的实根个数是（　　）
分析：方程的左边对应一个函数，作出它的图象是位于x轴上方的曲线，由抛物线y=x2-5x+4变换而来，而方程的右边对应一条经过点（2.5，0）的直线，讨论斜率k的正负，观察两个图象的交点个数，不难选出正确答案．
解答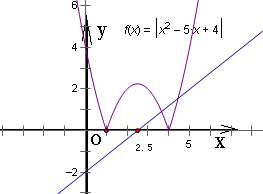：解：记f（x）=|x2-5x+4|，作出它的图象如图
该图象是由抛物线y=x2-5x+4将x轴下方的部分翻折到x轴上方
而x轴上方的部分不变而来的
直线y=k（x-
5
2
）是一条经过点（2.5，0）的直线
观察图象不难发现，当k=0时，两曲线交点
为（1，0）和（4，0），两个交点
而k＞0或k＜0时，均可得到两曲线在x轴上方有两个公共点
因此可得，不论k是正数、负数还是0，均可得到两曲线有两个公共点
故选B
点评：本题考查了函数与方程根的个数问题，属于基础题．数形结合是此类问题的常用方法，本题还考查了直线方程的基本量的特性，是一道不错的考题．
练习册系列答案
相关题目
（2009•湖北模拟）半径为1的球面上有A、B、C三点，其中点A与B、C两点间的球面距离均为
π
2
，B、C两点间的球面距离均为
π
3
，则球心到平面ABC的距离为（　　）
（2009•湖北模拟）已知数列{an}满足a1=1，an+1=
1
2
an+n(n为奇数)
an-2n(n为偶数)
且bn=a2n-2（n∈N*）
（1）求a2，a3，a4；
（2）求证：数列{bn}是等比数列，并求其通项公式；
（3）若Cn=-nbn，Sn为为数列{Cn}的前n项和，求Sn-2．
（2009•湖北模拟）已知命题p：|x|＜2，命题q：x2-x-2＜0，则p是q的（　　）
（2009•湖北模拟）已知函数y=f（x）是R上的偶函数，对于x∈R都有f（x-6）=f（x）+f（3）成立，且f（0）=-2，当x1，x2∈[0，3]，且x1≠x2时，都有
f(x1)-f(x2)x1-x2
＞0．则给出下列命题：
①f（2010）=-2；
②函数y=f（x）图象的一条对称轴为x=-6；
③函数y=f（x）在[-9，-6]上为增函数；
④方程f（x）=0在[-9，9]上有4个根．
其中正确命题的序号是
①②④
①②④
．（请将你认为是真命题的序号都填上）
（2009•湖北模拟）若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，例如解析式为y=2x2+1，值域为{9}的“孪生函数”三个：
（1）y=2x2+1，x∈{-2}；（2）y=2x2+1，x∈{2}；（3）y=2x2+1，x∈{-2，2}．
那么函数解析式为y=2x2+1，值域为{1，5}的“孪生函数”共有（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网