题目内容
设a=log3π，b=logπ3，c=log34，则a，b，c的大小顺序是________．（用“＜”连接）
b＜a＜c
分析：由a=log3π＞log33=1，b=logπ3＜logππ=1，c=log34＞log3π=a，能够比较a，b，c的大小．
解答：∵a=log3π＞log33=1，
b=logπ3＜logππ=1，
c=log34＞log3π=a，
∴b＜a＜c．
故答案为：b＜a＜c．
点评：本题考查对数值大小的比较，是基础题．解题时要认真审题，仔细解答，注意对数函数性质的灵活运用．
分析：由a=log3π＞log33=1，b=logπ3＜logππ=1，c=log34＞log3π=a，能够比较a，b，c的大小．
解答：∵a=log3π＞log33=1，
b=logπ3＜logππ=1，
c=log34＞log3π=a，
∴b＜a＜c．
故答案为：b＜a＜c．
点评：本题考查对数值大小的比较，是基础题．解题时要认真审题，仔细解答，注意对数函数性质的灵活运用．
练习册系列答案
名校课堂系列答案
相关题目
设a=log3π，b=log2
，c=log3
，则（ ）
| 3 |
| 2 |
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞a＞c |
| D、b＞c＞a |
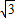，c=log
，则（ ）