题目内容
（2009•济宁一模）已知向量
=（1，2），
=（0，1），设
=
+k
，
=2
-
，若
∥
，则实数k的值为（ ）
| a |
| b |
| u |
| a |
| b |
| v |
| a |
| b |
| u |
| v |
分析：先表示出向量
+k
和向量2
-
，根据共线定理的坐标表示即可解出实数k的值．
| a |
| b |
| a |
| b |
解答：解：∵
=（1，2），
=（0，1），
∴
+k
=（1，2+k），2
-
=（2，3），
（
+k
）∥（2
-
）得，1×3-（2+k）×2=0，
∴k=-
．
故选B．
| a |
| b |
∴
| a |
| b |
| a |
| b |
（
| a |
| b |
| a |
| b |
∴k=-
| 1 |
| 2 |
故选B．
点评：本题主要考查平面向量的坐标运算和共线定理、平面向量共线（平行）的坐标表示，属基础题．
练习册系列答案
相关题目
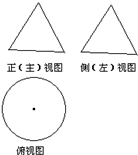（2009•济宁一模）一个几何体的三视图如图所示，其中正视图与侧视图都是边长为2的正三角形，则这个几何体的侧面积为（ ）
（2009•济宁一模）如图，在三棱柱ABC-A1B1C1中，所有的棱长都为2，∠A1AC=60°