题目内容
已知圆C的圆心与抛物线y2=4x的焦点关于直线y=x对称.直线4x-3y-2=0与圆C相交于A、B两点,且|AB|=6,则圆C的方程为.分析:先根据抛物线方程求得焦点坐标,进而求得圆心,进而求得圆心到直线4x-3y-2=0的距离,根据勾股定理求得圆的半径.则圆的方程可得.
解答:解:依题意可知抛物线的焦点为(1,0),
∵圆C的圆心与抛物线y2=4x的焦点关于直线y=x对称.
所以圆心坐标为(0,1),
∴r2=32+
=10,
圆C的方程为x2+(y-1)2=10
故答案为x2+(y-1)2=10
∵圆C的圆心与抛物线y2=4x的焦点关于直线y=x对称.
所以圆心坐标为(0,1),
∴r2=32+
| (0-3-2)2 |
| 52 |
圆C的方程为x2+(y-1)2=10
故答案为x2+(y-1)2=10
点评:本题主要考查了抛物线的应用.涉及了圆的基本性质,对称性问题,点到直线的距离,数形结合思想等问题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
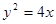 的焦点关于直线
的焦点关于直线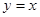 对称,直线
对称,直线 与圆C相交于
与圆C相交于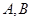 两点,且
两点,且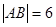 ,则圆C的方程为
.
,则圆C的方程为
.