题目内容
已知圆C的圆心与抛物线y2=4x的焦点关于y轴对称,又直线4x-3y-6=0与圆C相切,则圆C的标准方程为
(x+1)2+y2=4
(x+1)2+y2=4
.分析:确定抛物线的焦点坐标,从而扩大圆心坐标,利用直线4x-3y-6=0与圆C相切,可求圆的半径,从而可求圆C的标准方程.
解答:解:抛物线y2=4x的焦点坐标为(1,0),
∵圆C的圆心与抛物线y2=4x的焦点关于y轴对称,
∴C(-1,0)
∴C到直线4x-3y-6=0的距离为d=
=2
∴圆C的标准方程为(x+1)2+y2=4
故答案为:(x+1)2+y2=4
∵圆C的圆心与抛物线y2=4x的焦点关于y轴对称,
∴C(-1,0)
∴C到直线4x-3y-6=0的距离为d=
| |-4-0-6| |
| 5 |
∴圆C的标准方程为(x+1)2+y2=4
故答案为:(x+1)2+y2=4
点评:本题考查抛物线的性质,考查圆的标准方程,确定圆心坐标与半径是关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
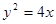 的焦点关于直线
的焦点关于直线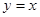 对称,直线
对称,直线 与圆C相交于
与圆C相交于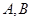 两点,且
两点,且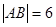 ,则圆C的方程为
.
,则圆C的方程为
.