题目内容
已知函数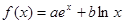 (
(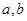 为常实数)的定义域为
为常实数)的定义域为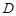 ,关于函数
,关于函数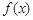 给出下列命题:
给出下列命题:
①对于任意的正数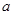 ,存在正数
,存在正数 ,使得对于任意的
,使得对于任意的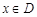 ,都有
,都有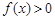 .
.
②当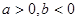 时,函数
时,函数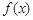 存在最小值;
存在最小值;
③若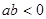 时,则
时,则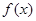 一定存在极值点;
一定存在极值点;
④若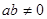 时,方程
时,方程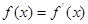 在区间(1,2)内有唯一解.
在区间(1,2)内有唯一解.
其中正确命题的序号是 .
【答案】
②③④.
【解析】
试题分析:由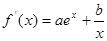 ,①若
,①若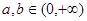 则
则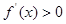 ,则
,则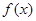 单调递增当
单调递增当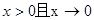 时
时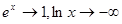 ,所以不能保证任意的
,所以不能保证任意的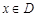 ,都有
,都有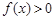 .②当
.②当 时,
时,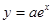 与
与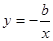 的图象知在第一象限有交点
的图象知在第一象限有交点 且在
且在 ,当
,当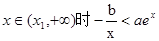 所以
所以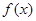 在定义域内先减后增,故存在最小值.③相当于在②条件下提取一负号即可,正确;④由
在定义域内先减后增,故存在最小值.③相当于在②条件下提取一负号即可,正确;④由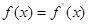 得
得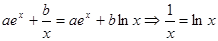 即
即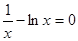 的解即为
的解即为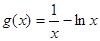 的零点,而
的零点,而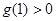 且
且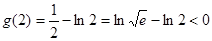 ,所以正确.
,所以正确.
考点:1.导数与函数的性质(单调性、极值、最值);2.函数的零点与方程的根.

练习册系列答案
相关题目