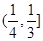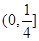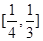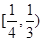题目内容
定义在R上的偶函数 ,对任意
,对任意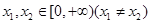 ,有
,有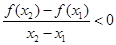 ,则 ( ).
,则 ( ).
A.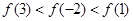 | B.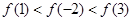 |
C.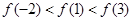 | D.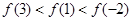 |
A
解析试题分析:根据选择支提供的信息,本题是要考察函数 的单调性,由于
的单调性,由于 是偶函数,故我们只要研究
是偶函数,故我们只要研究 在
在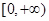 上的单调性即可.对
上的单调性即可.对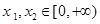 ,不忍设
,不忍设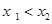 ,则
,则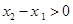 ,由已知
,由已知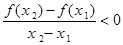 ,得
,得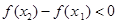 ,即
,即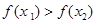 ,所以
,所以 在区间
在区间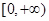 上是减函数,从而
上是减函数,从而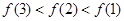 ,再由
,再由 为偶函数知正确答案为A.
为偶函数知正确答案为A.
考点:函数的单调性.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
函数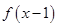 是
是 上的奇函数,
上的奇函数,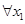 、
、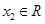 ,
,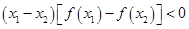 ,则
,则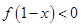 的解集是( )
的解集是( )
A.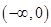 | B.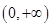 | C. | D.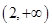 |
定义在R上的可导函数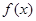 ,已知
,已知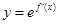 的图象如图所示,则
的图象如图所示,则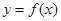 的增区间是( )
的增区间是( )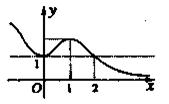
A.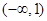 | B.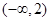 | C.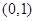 | D.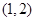 |
若函数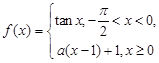 在
在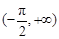 上单调递增,则实数
上单调递增,则实数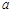 的取值范围( )
的取值范围( )
A.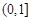 | B.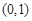 | C.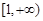 | D.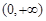 |
函数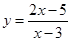 的值域是
的值域是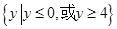 ,则此函数的定义域为( )
,则此函数的定义域为( )
A.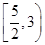 | B.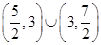 | C.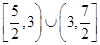 | D.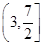 |
函数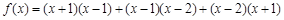 的两个零点分别位于区间
的两个零点分别位于区间
A.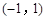 和 和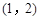 内 内 | B.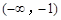 和 和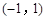 内 内 |
C.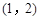 和 和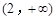 内 内 | D.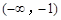 和 和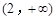 内 内 |
函数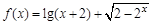 的定义域为( )
的定义域为( )
A.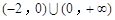 | B.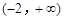 |
C.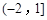 | D.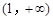 |
设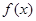 是定义在
是定义在 上的一个函数,则函数
上的一个函数,则函数 在
在 上一定是( )
上一定是( )
| A.奇函数 | B.偶函数 |
| C.既是奇函数又是偶函数 | D.非奇非偶函数 |
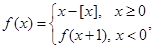 其中
其中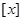 表示不超过
表示不超过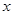 的最大整数,如
的最大整数,如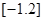 =-2,
=-2,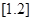 =1,
=1,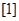 =1,
=1, 与函数y=
与函数y= 的图象恰有三个不同的交点,则
的图象恰有三个不同的交点,则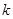 的取值范围是 ( )
的取值范围是 ( )