题目内容
【题目】已知向量 
=（2cos2x， 
）， 
=（1，sin2x），函数f（x）= ﹣1．
（1）当x= 
时，求|a﹣b|的值；
（2）求函数f（x）的最小正周期以及单调递增区间；
（3）求方程f（x）=k，（0＜k＜2），在[﹣ 
， 
]内的所有实数根之和．
【答案】
（1）
解：由向量 
=（2cos2x， 
）， 
=（1，sin2x），
则：a﹣b=（2cos2x﹣1， 
sin2x）
当x= 
时，a﹣b=（2cos2 ﹣1， sin2× ）
=（0， ）
那么：|a﹣b|= 
（2）
解：f（x）=ab﹣1=1×2cos2x+ 
sin2x
= 
=1+cos2x+ sin2x﹣1
=2sin（2x+ 
）
∴最小正周期T= 
由sinx的图象和性质，可知x 
，（k∈Z）是增区间．
∴2x+ 
是增区间，即： 
，（k∈Z）
解得： 
，（k∈Z）
所以，f（x）的单调增区间为： 
，（k∈Z）
（3）
解：由方程f（x）=k，（0＜k＜2），得 
．
∵ 
的周期T=π，又 
，
∴ 在 
内有2个周期．
∵ 
，∴方程 在 内有4个交点，即有4个实根．
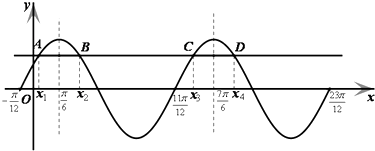
根据图象的对称性，有 
， 
，
∴所有实数根之和=x1+x2+x3+x4+x5+x6= 
．
【解析】（1）根据平面向量加减的运算法则求出a﹣b，化简，将x= 带入，求模长．（2）根据平面向量乘积的运算法则求出f（x），将其化简，结合三角函数的图象和性质即可得到答案．（3）利用三角函数的图象和性质，在[﹣ 
， 
]内求出方程f（x）=k时，x的值，即可解决问题．
【题目】王府井百货分店今年春节期间，消费达到一定标准的顾客可进行一次抽奖活动，随着抽奖活动的有效开展，参与抽奖活动的人数越来越多，该分店经理对春节前7天参加抽奖活动的人数进行统计， 
表示第
天参加抽奖活动的人数，得到统计表格如下：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
经过进一步统计分析，发现
与
具有线性相关关系．
（1）请根据上表提供的数据，用最小二乘法求出
关于
的线性回归方程
；
（2）判断变量
与
之间是正相关还是负相关；
（3）若该活动只持续10天，估计共有多少名顾客参加抽奖．
参与公式： 
， 
， 
．
