题目内容
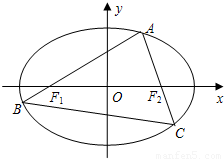
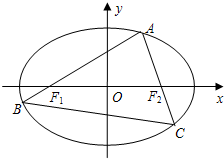 如图,A为椭圆
如图,A为椭圆 (a>b>0)上的一个动点,弦AB,AC分别过焦点F1,F2.当AC垂直于x轴时,恰好|AF1|:|AF2|=3:1.
(a>b>0)上的一个动点,弦AB,AC分别过焦点F1,F2.当AC垂直于x轴时,恰好|AF1|:|AF2|=3:1.
(1)求该椭圆的离心率;
(2)设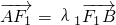 ,
,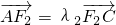 ,试判断λ1+λ2是否为定值?若是,则求出该定值;若不是,请说明理由.
,试判断λ1+λ2是否为定值?若是,则求出该定值;若不是,请说明理由.
解:(1)当AC垂直于x轴时,|AF1|:|AF2|=3:1,由|AF1|+|AF2|=2a,
得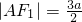 ,
,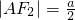 在Rt△AF1F2中,|AF1|2=|AF2|2+(2c)2
在Rt△AF1F2中,|AF1|2=|AF2|2+(2c)2
解得 e= .
.
(2)由e= ,则
,则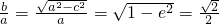 ,b=c.
,b=c.
焦点坐标为F1(-b,0),F2(b,0),则椭圆方程为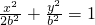 ,
,
化简有x2+2y2=2b2.
设A(x0,y0),B(x1,y1),C(x2,y2),
①若直线AC⊥x轴,x0=b,λ2=1,
∴λ1+λ2=6.
②若直线AC的斜率存在,则直线AC方程为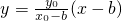
代入椭圆方程有(3b2-2bx0)y2+2by0(x0-b)y-b2y02=0.
由韦达定理得: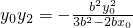 ,∴
,∴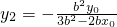
所以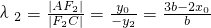 ,
,
同理可得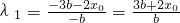
故λ1+λ2=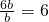 .综上所述:λ1+λ2是定值6.
.综上所述:λ1+λ2是定值6.
分析:(1)由|AF1|:|AF2|=3:1,及椭圆定义|AF1|+|AF2|=2a,可求AF1,AF2,在在Rt△AF1F2中,利用勾股定理可求
(2)由(1)可得b=c.椭圆方程为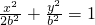 ,设A(x0,y0),B(x1,y1),C(x2,y2),
,设A(x0,y0),B(x1,y1),C(x2,y2),
①若直线AC⊥x轴容易求解②若直线AC的斜率存在,则直线AC方程为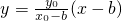 代入椭圆方程,结合韦达定理可求
代入椭圆方程,结合韦达定理可求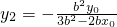 ,从而可求
,从而可求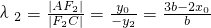 ,同理可得
,同理可得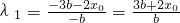 ,代入可求
,代入可求
点评:本题主要考查了利用椭圆得性质及椭圆的定义求解椭圆的方程,直线与椭圆的相交中方程思想的应用,这是处理直线与椭圆位置关系的通法,但要注意基本运算的考查
得
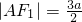 ,
,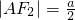 在Rt△AF1F2中,|AF1|2=|AF2|2+(2c)2
在Rt△AF1F2中,|AF1|2=|AF2|2+(2c)2解得 e=
 .
.(2)由e=
 ,则
,则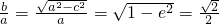 ,b=c.
,b=c.焦点坐标为F1(-b,0),F2(b,0),则椭圆方程为
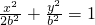 ,
,化简有x2+2y2=2b2.
设A(x0,y0),B(x1,y1),C(x2,y2),
①若直线AC⊥x轴,x0=b,λ2=1,

∴λ1+λ2=6.
②若直线AC的斜率存在,则直线AC方程为
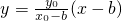
代入椭圆方程有(3b2-2bx0)y2+2by0(x0-b)y-b2y02=0.
由韦达定理得:
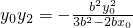 ,∴
,∴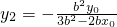
所以
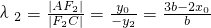 ,
,同理可得
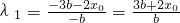
故λ1+λ2=
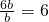 .综上所述:λ1+λ2是定值6.
.综上所述:λ1+λ2是定值6.分析:(1)由|AF1|:|AF2|=3:1,及椭圆定义|AF1|+|AF2|=2a,可求AF1,AF2,在在Rt△AF1F2中,利用勾股定理可求
(2)由(1)可得b=c.椭圆方程为
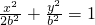 ,设A(x0,y0),B(x1,y1),C(x2,y2),
,设A(x0,y0),B(x1,y1),C(x2,y2),①若直线AC⊥x轴容易求解②若直线AC的斜率存在,则直线AC方程为
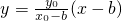 代入椭圆方程,结合韦达定理可求
代入椭圆方程,结合韦达定理可求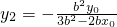 ,从而可求
,从而可求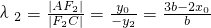 ,同理可得
,同理可得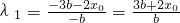 ,代入可求
,代入可求点评:本题主要考查了利用椭圆得性质及椭圆的定义求解椭圆的方程,直线与椭圆的相交中方程思想的应用,这是处理直线与椭圆位置关系的通法,但要注意基本运算的考查

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
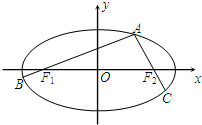 如图,A为椭圆
如图,A为椭圆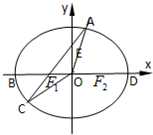 (A题)如图,在椭圆
(A题)如图,在椭圆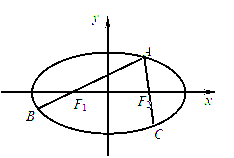 如图,A为椭圆
如图,A为椭圆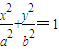 (a>b>0)上的一个动点,弦AB,AC分别过焦点F1,F2.当AC垂直于x轴时,恰好|AF1|:|AF2|=3:1.
(a>b>0)上的一个动点,弦AB,AC分别过焦点F1,F2.当AC垂直于x轴时,恰好|AF1|:|AF2|=3:1.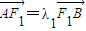 ,
,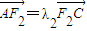 ,试判断λ1+λ2是否为定值?若是,则求出该定值;若不是,请说明理由.
,试判断λ1+λ2是否为定值?若是,则求出该定值;若不是,请说明理由.