题目内容
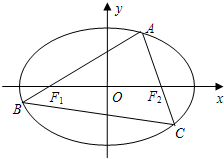
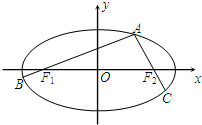 如图,A为椭圆
如图,A为椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的离心率;
(2)设
| AF1 |
| F1B |
| AF2 |
| F2C |
分析:(1)设|AF2|=m,则|AF1|=3m.由题设及椭圆定义得
.消去m,再利用椭圆离心率计算公式即可得出.
(2)由(1)知:b2=c2=
a2,可得椭圆方程可化为x2+2y2=2c2.
设A(x0,y0),B(x1,y1),C(x2,y2),则x02+2y02=2c2.
①若A为椭圆的长轴端点,则λ1=
, λ2=
,或λ1=
, λ2=
,即可得出;
②若A为椭圆上异于长轴端点的任意一点,则由
=λ1
,
=λ2
得λ1=-
, λ2=-
,分别把直线AF1,AF2的方程与椭圆方程联立,得到根与系数的关系,即可用x0,y0表示λ1,λ2即可.
|
(2)由(1)知:b2=c2=
| 1 |
| 2 |
设A(x0,y0),B(x1,y1),C(x2,y2),则x02+2y02=2c2.
①若A为椭圆的长轴端点,则λ1=
| a+c |
| a-c |
| a-c |
| a+c |
| a-c |
| a+c |
| a+c |
| a-c |
②若A为椭圆上异于长轴端点的任意一点,则由
| AF1 |
| F1B |
| AF2 |
| F2C |
| y0 |
| y1 |
| y0 |
| y2 |
解答:解:(1)设|AF2|=m,则|AF1|=3m.
由题设及椭圆定义得
.
消去m得a2=2c2,所以离心率e=
.
(2)由(1)知:b2=c2=
a2,所以椭圆方程可化为x2+2y2=2c2.
设A(x0,y0),B(x1,y1),C(x2,y2),则x02+2y02=2c2.
①若A为椭圆的长轴端点,则λ1=
, λ2=
,或λ1=
, λ2=
,
所以λ1+λ2=
=6.
②若A为椭圆上异于长轴端点的任意一点,则由
=λ1
,
=λ2
得λ1=-
, λ2=-
,
所以λ1+λ2=-y0(
+
).
又直线AF1的方程为x+c=
y,
由
得[2y02+(x0+c)2]y2-2cy0(x0+c)y-c2y02=0.
∵x02+2y02=2c2,
∴(3c+2x0)y2-2y0(x0+c)y-cy02=0,
由韦达定理得y0y1=-
,∴y1=-
,
由对称性得y2=
.
所以λ1+λ2=-y0(
+
)=-y0(-
+
)=6.
综上可得,当A点在椭圆上运动时,λ1+λ2为定值6.
由题设及椭圆定义得
|
消去m得a2=2c2,所以离心率e=
| ||
| 2 |
(2)由(1)知:b2=c2=
| 1 |
| 2 |
设A(x0,y0),B(x1,y1),C(x2,y2),则x02+2y02=2c2.
①若A为椭圆的长轴端点,则λ1=
| a+c |
| a-c |
| a-c |
| a+c |
| a-c |
| a+c |
| a+c |
| a-c |
所以λ1+λ2=
| 2(a2+c2) |
| a2-c2 |
②若A为椭圆上异于长轴端点的任意一点,则由
| AF1 |
| F1B |
| AF2 |
| F2C |
| y0 |
| y1 |
| y0 |
| y2 |
所以λ1+λ2=-y0(
| 1 |
| y1 |
| 1 |
| y2 |
又直线AF1的方程为x+c=
| x0+c |
| y0 |
由
|
∵x02+2y02=2c2,
∴(3c+2x0)y2-2y0(x0+c)y-cy02=0,
由韦达定理得y0y1=-
| cy02 |
| 3c+2x0 |
| cy0 |
| 3c+2x0 |
由对称性得y2=
| cy0 |
| -3c+2x0 |
所以λ1+λ2=-y0(
| 1 |
| y1 |
| 1 |
| y2 |
| 3c+2x0 |
| cy0 |
| -3c+2x0 |
| cy0 |
综上可得,当A点在椭圆上运动时,λ1+λ2为定值6.
点评:熟练掌握椭圆的定义标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量的运算及其相等、分类讨论思想方法等是解题的关键.

练习册系列答案
相关题目
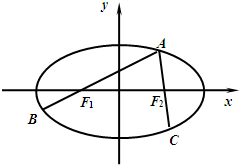 如图,A为椭圆
如图,A为椭圆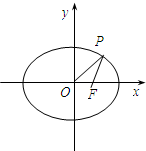 如图,F为椭圆
如图,F为椭圆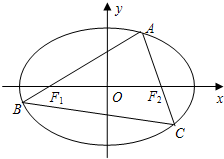 如图,A为椭圆
如图,A为椭圆